Oberstufe: Differential- und Integralrechnung

Oberstufenskript Differential- und Integralrechnung für Grund- und Leistungskurse von Jürgen Rohde

zurück zum INHALT

 9.4 Die Existenz von Inhaltsfunktionen

 
10. Eigenschaften L-stetiger Funktionen

Man vergegenwärtige sich noch einmal die lokale und globale Definition der L-Stetigkeit von Funktionen und wiederhole elementare Eigenschaften L-stetiger Funktionen. (siehe Definitionen in 9.2)

Weil die Sekanten-Steigungen L-stetiger Funktionen beschränkt sind, ist der folgende Satz plausibel:
 

	Satz 1	Wenn  f  über  [ a | b ]  L-stetig, so auch beschränkt.

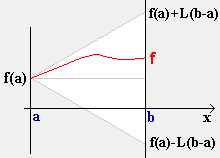Beweis:
Nach Voraussetzung gibt es eine Zahl  L , so dass in  [ a | b ] 

 | f (x) - f (a) |   L · | x - a |   L · ( b - a ) 

ist. Hieraus folgt

 f (a) - L ( b - a )   f (x)   f (a) + L ( b - a ) 

womit der Beweis fertig ist, denn links und rechts stehen feste Zahlen (Konstante).
 
Es wird hier der angekündigte Beweis von Satz 1 in 9.2 nachgeholt.

	Satz 2	Wenn  f   L-differenzierbar in  [ a | b ] , so auch L-stetig.

Beweis:

Nach Voraussetzung gibt es eine Konstante  K , so dass für alle  x  und  x0  aus  [ a | b ]  gilt:    | f (x) - f (x0) - f ' (x0) · ( x - x0 ) |   K · ( x - x0 )² Nach der Dreiecksungleichung folgt ( vergleiche Satz 11 in 1.2 )    | f (x) - f (x0) | - | f ' (x0) | · | x - x0 |   K · | x - x0 |² und weiter    | f (x) - f (x0) |   [ | f ' (x0) | + K · | x - x0 | ] · | x - x0 | und    | f (x) - f (x0) |   | Sf ' + K · ( b - a ) | · | x - x0 |  , wobei Sf ' eine Schranke für  | f ' |  ist, welche nach dem folgenden Satz 3 existiert.

 

	Satz 3	Wenn die Funktion  f   L-differenzierbar ist in  [ a | b ] ,     dann ist die Ableitungsfunktion  f '  in  [ a | b ]  L-stetig.

Beweis:

Für je zwei Zahlen  u, v  aus  I  gilt nach Voraussetzung für ein  K > 0     f ' (u) · ( v - u ) = f (v) - f (u) - R1 (u,v)     mit  | R1 |   K ( v - u )² und    f ' (v) · ( u - v ) = f (u) - f (v) - R2 (u,v)     mit  | R2 |   K ( u - v )²  . Durch Addition der Gleichungen erhält man    [ f ' (u) - f ' (v) ] · ( v - u ) = - ( R1 + R2 ) und hieraus    | f ' (u) - f ' (v) |    2 K · | u - v |     für  u v . Da die Ungleichung für  u = v  ohnehin richtig ist, ist damit die L-Stetigkeit von  f '  bewiesen.

Bemerkung:

Aus Satz 3 folgt natürlich: Wenn  f '  existiert, dann ist  f '  auch beschränkt. ( Vergleiche Satz 2 )

L-Stetigkeit verhindert, dass Funktionskurven Sprünge haben. Daher ist zu vermuten, dass der Wertbereich einer L-stetigen Funktion lückenlos ist, wenn es der Definitionsbereich ist. Etwas genauer: Jeder Zwischenwert zwischen  f (a)  und  f (b)  ist auch Funktionswert über  [ a | b ] . Es werde in der folgenden Form bewiesen:
 

	Satz 4	( Nullstellensatz )
		Die Funktion sei in  [ a | b ]  L-stetig und  f (a)  ·  f (b)  < 0 .     Dann gibt es eine Stelle  z  ] a | b [  mit  f (z) = 0  .

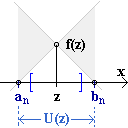
Beweis	Ohne Beschränkung der Allgemeinheit sei  f (a) < 0  und  f (b) > 0 .
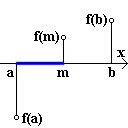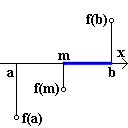	Fig. 1	Fig. 2	Fig. 3
	m  sei die Mitte von  [ a | b ] , also  m = ½( a + b ) . Wenn  f (m) = 0 , ist  m  Nullstelle und der Beweis fertig. Wenn  f (m) > 0 , betrachten wir das Intervall  [ a | m ] . (Fig. 1) Wenn  f (m) < 0 , betrachten wir das Intervall  [ m | b ] . (Fig. 2) Dieses Verfahren setzen wir fort. Entweder findet man nach endlich vielen Schritten zufällig eine Nullstelle, oder man erhält eine unendliche Folge ineinandergeschachtelter Intervalle, deren Länge  ( b - a ) / 2n-1  beliebig klein wird. Nach dem Axiom der Intervallschachtelung gibt es genau eine reelle Zahl  z , die in allen Intervallen enthalten ist. Es ist noch zu zeigen, dass  f (z) = 0  ist. Dazu erinnere man sich daran, dass die Intervalle der Schachtelung so ausgewählt wurden, dass der Funktionswert am linken Intervallende negativ, am rechten positiv ist. Wäre nun  f (z) > 0 , so gäbe es wegen der L-Stetigkeit von  f  eine Umgebung  U (z) , worüber  f (x) > 0  ist. ( Vergleiche Fig. 3 ) Weil aber die Länge der Intervalle der Schachtelung beliebig klein wird, gibt es ein Intervall  [ an | bn ]  der Schachtelung, welches (mit allen folgenden Intervallen) ganz in  U (z)  liegt. Dann ist aber  f (an)  < 0  nach Kontruktion im Widerspruch zu  f (x)  < 0  in ganz  U (z) . Ebenso widerlegt man  f (z)  < 0

 

	Satz 5	Zwischenwertsatz
		Die Funktion  f  sei über  [ a | b ]   L-stetig und  Y  eine Zahl zwischen  f (a)  und  f (b) . Dann gibt es eine Zahl  Z  mit  f (Z) = Y .

Beweis von Satz 5 siehe Aufgabe 9.

Aufgaben zu 10.

weiter zu    11. Mittelwertsätze  

 zurück zu MATHEMATIK Übersicht