 |
AUFGABEN zu Differential-/Integralrechnung
|
Aufgaben zu
10. Eigenschaften L-stetiger Funktionen
- Zeige: Wenn f L-stetig in [ a | b ] und z
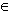 [ a | b ] und f (z) > 0 ist,
[ a | b ] und f (z) > 0 ist,
| |
dann ist f (x) > 0 in ] z - |
f (z)
L |
| z + |
f (z)
L |
[ |
 |
[ a | b ] . |
- Geben Sie unter den Bedingungen der 1. Aufgabe eine Umgebung an,
worüber f (x) > ½ f (z) .
- Zeige: x
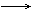 1/x ist L-stetig in
[ 1 | 10 ] , in [ 0,1 | 1 ] .
1/x ist L-stetig in
[ 1 | 10 ] , in [ 0,1 | 1 ] .
- Zeige: x
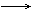 1/x ist L-stetig in
[ a | b ] , wenn 0 nicht in [ a | b ] .
1/x ist L-stetig in
[ a | b ] , wenn 0 nicht in [ a | b ] .
- Zeige: x
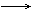
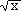 ist L-stetig [ 0,1 | 20 ] .
ist L-stetig [ 0,1 | 20 ] .
- Zeige: x
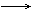
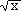 ist bei x = 0 nicht L-stetig, auch nicht von rechts.
ist bei x = 0 nicht L-stetig, auch nicht von rechts.
- Zeige: x
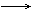 1/x
ist bei x = 0 nicht L-stetig .
1/x
ist bei x = 0 nicht L-stetig .
- Zeige durch vollständige Induktion: Wenn f über I L-stetig ist,
dann auch f n .
- Beweise:
| | Satz 5 |
Zwischenwertsatz |
Die Funktion f sei über [ a | b ] L-stetig
und Y eine Zahl zwischen f (a) und f (b) .
Dann gibt es eine Zahl Z mit f (Z) = Y . |
Hinweis zum Beweis:
Zeige, dass die Funktion f (x) - Y
die Voraussetzungen des Nullstellensatzes erfüllt.
- Unter welchen Bedingungen ist mit der Funktion f auch die Funktion 1/f L-stetig.
Führe den entsprechenden Beweis.
- Zeige: Ganzrationale Funktionen ungeraden Grades haben mindestens eine Nullstelle.
- Beweise den Nullstellensatz auch unter Benutzung von
Aufgabe 4. aus 9.1 . Zeige im Einzelnen:
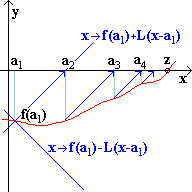 |
|
Die Folge mit |
| a1 = a |
| a2 = a1 - | f (a1) |
 |
| L |
·
·
· |
| an = an-1 - | f (an-1) |
 |
| L |
·
·
· |
ist monoton steigend und beschränkt. Für ihren Grenzwert gilt f (z) = 0 .
- Beweise z.B. mit Hilfe von 12.:
Wenn f über [ a | b ] L-stetig und f (x) > 0 in [ a | b ] ,
dann gibt es eine positive Zahl c , so dass sogar
f (x) 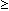 c ( > 0 )
in [ a | b ] ist.
c ( > 0 )
in [ a | b ] ist.
- Beweisen Sie diesen Satz auch indirekt, indem Sie zeigen:
Wenn es keine positive untere Schranke von f über [ a | b ] gibt,
dann hat f in [ a | b ] eine Nullstelle.
- f und g seien über [ a | b ] L-stetig und
f (a) > g (a) und f (b) < g (b) .
Dann haben f und g mindestens einen Schnittpunkt in [ a | b ] .
weitere Aufgaben zu
11. Mittelwertsätze
 zurück zu MATHEMATIK Übersicht
zurück zu MATHEMATIK Übersicht
![]()