AUFGABEN zu Differential-/Integralrechnung

Aufgaben zu
11. Mittelwertsätze

1. Beweise den Mittelwertsatz der Differentialrechnung .
   

   Zum Beweis zeige, dass  f (x) - f (a) +	f (b) - f (a)     b - a	( x - a )  =  h (x)
   die Voraussetzungen des Satzes von Rolle erfüllt.

2. Beweise den verallgemeinerten Mittelwertsatz :
    f  und  g  seien in  [ a | b ]  L-differenzierbar und  a 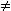b .
   g ' (x)  sei in  [ a | b ]  ungleich  0 .
   

   Dann gibt es ein  z 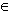 ] a | b [  mit

   f (b) - f (a) g (b) - g (a)

   =

   f ' (z) g' (z)

   Anleitung zum Beweis: Zeige, dass die Funktion  h  mit
         h (x) = ( f (a) - f (b) ) · g (x) - ( g (a) - g (b) ) · f (x)
   die Voraussetzungen des Satzes von Rolle erfüllt.

3. Zeige, dass aus dem Mittelwertsatz der Schrankensatz folgt. Inwiefern geht der Mittelwertsatz über den letzteren hinaus?

4. Zeige: Wenn ein Fahrzeug die Durchschnittsgeschwindigkeit  30 km/h  hat, dann ist ist auch die Momentangeschwindigkeit mindestens einmal genau  30 km/h .

5. Es sei  f (x) = 3 x³ - 4 x² + 6 x - 3  über  [ -2 | 4 ] . Welche Zahlen aus  [ -2 | 4 ]  erfüllen die Forderung des Mittelwertsatzes?

6. Es sei  f (x) = 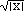  über  [ -4 | 4 ] . Warum funktioniert hier der Satz von Rolle nicht?

7. Zeige: Für jede quadratische Funktion  y = a x² + b x + c  ist der Wert  z  des Mittelwertsatzes der Mittelpunkt des Intervalls.

8. Nicht immer gibt es zu einer Tangente eine parallele Sehne. Besipiele?

9. Beweise den Mittelwertsatz der Integralrechnung :
   Es sei  f  in  [ a | b ]  L-stetig.

   Dann gibt es in  [ a | b ]  eine Zahl  z  mit

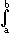   f (x) dx = ( b - a ) · f (z)  .

   ( Zeichnung ! )

weitere Aufgaben zu    12. Verkettung von Funktionen - Ableitungsregeln  

 zurück zu MATHEMATIK Übersicht