Oberstufe: Differential- und Integralrechnung

Oberstufenskript Differential- und Integralrechnung für Grund- und Leistungskurse von Jürgen Rohde

zurück zum INHALT

 10. Eigenschaften L-stetiger Funktionen

 
11. Mittelwertsätze

Mit Hilfe des Zwischenwertsatzes ( 10. ) für stetige Funktionen gelingt es, den Schrankensatz ( 7.2 ) zu verschärfen.
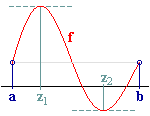
Zunächst sei  f  in  [ a | b ]   L-differenzierbar und  f (a)  =  f (b)  (Fig. 1).
Anschaulich ist es plausibel, dass es im Inneren des Intervalls  [ a | b ]  mindestens einen Punkt mit einer Tangente parallel zur x-Achse gibt.
 

	Satz 1	Satz von Rolle
		Es sei  f  in  [ a | b ]  L-differenzierbar und  f (a)  =  f (b) . Dann gibt es mindestens eine Stelle  z   ] a | b [  mit  f ' (z) = 0  .

Beweis:

Wenn  f ' (x) = 0  für alle  x  [ a | b ] , ist der Beweis fertig. Es sei also  f '  nicht überall Null, etwa an wenigstens einer Stelle  u  positiv. Gäbe es keine negativen  f ' -Werte, wäre  f  in  [ a | b ]  monoton steigend und sogar  f (a) < f (b)  im Widerspruch zur Voraussetzung, also gibt es ein  v   [a | b ]  mit  f ' (v)  < 0 . Nach Satz 3 in 10. ist  f '   L-stetig in  [ a | b ] . Also gibt es nach dem Nullstellensatz eine Stelle  z  zwischen  u  und  v  mit  f ' (z) = 0

 

	Satz 2	Mittelwertsatz der Differentialrechnung
		Wenn die Funktion  f  in  [ a | b ]  L-differenzierbar ist,
		dann gibt es eine Stelle  z   ] a | b [  mit  f ' (z) =	f (b) - f (a)     b - a	.

Beweis: als Aufgabe 1

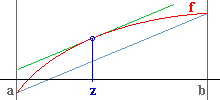
In Worten besagt der Satz 2, dass eine über einem abgeschlossenen Intervall differenzierbare Kurve mindestens eine Tangente hat, die parallel zur Sekante durch die Kurvenpunkte über den Intervallenden verläuft.

 

	Satz 3	Mittelwertsatz der Integralrechnung
		Es sei  f  in  [ a | b ]  L-stetig.
		Dann gibt es in  [ a | b ]  eine Zahl  z  mit		f (x) dx = ( b - a ) · f (z)  .

Beweis: als Aufgabe 9
 

Aufgaben zu 11.

weiter zu    12. Verkettung von Funktionen - Ableitungsregeln  

 zurück zu MATHEMATIK Übersicht