| Oberstufe: Differential- und Integralrechnung |
| Oberstufenskript Differential- und Integralrechnung für Grund- und Leistungskurse von Jürgen Rohde |
Auf Intervalle bezieht sich ein etwas modifizierter Monotoniebegriff:
Definition
| Die Funktion f heißt über dem Intervall I monoton steigend (monoton fallend), | |
| wenn für je zwei x1, x2 |
|
| x1 < x2 |
|
| f heißt über I streng monoton (fallend), | |
| wenn x1, x2 |
Nach Satz 2 aus 7.1 ist es naheliegend, so zu argumentieren:
Wenn an jeder Stelle x ![]() I f ' (x) > 0 ist,
dann steigt f überall in I .
Daher ist f in I monoton (sogar streng) steigend.
I f ' (x) > 0 ist,
dann steigt f überall in I .
Daher ist f in I monoton (sogar streng) steigend.
Das ist auch richtig,
nur erfordert der Beweis des letzten Schlusses einen höheren Aufwand als der Beweis des folgenden Satzes.
| Satz 3 | Globaler Monotoniesatz | |
|---|---|---|
| Wenn f ' |
Beweis: (Vorbemerkung: f ' ![]() 0 in I
0 in I
![]() für alle x
für alle x
![]() I gilt f ' (x)
I gilt f ' (x) ![]() 0 )
0 )
|
Es seien u, v Das Intervall [ u | v ] wird in n gleichlange Teilintervalle unterteilt mit den Teilpunkten |
|||||
| u = x0, x1, x2, x3, . . . , xn = v . | |||||
| Die Länge eines Teilintervalles sei h = x1 - x0 = x2 - x1 = | v - u n | . | |||
| Aus dem linken Teil der Ungleichungskette ( D in 7.1 Lokale Monotoniesätze) folgt | |||||
| (1) | f (x1) | also | |||
|---|---|---|---|---|---|
| (2) | f (x1) |
und entsprechend | |||
| (3) | f (x2) |
||||
| : | : | ||||
| : | : | ||||
| (n+1) | f (xn) |
||||
Durch Addition der n Ungleichungen (2) bis (n+1) folgt
f (x1) + f (x2) + . . . + f (xn) ![]() f (x0) + f (x1) + . . . + f (xn-1) - n · k h²
f (x0) + f (x1) + . . . + f (xn-1) - n · k h²
und daraus
f (v) ![]() f (u) - n k h²
f (u) - n k h²
und weiter
| f (v) |
k ( v - u )² n | . |
f (v) ![]() f (u) bzw.
f (u)
f (u) bzw.
f (u) ![]() f (v) ,
f (v) ,
womit der Beweis beendet ist.
Entsprechend kann man
| Satz 3* | ( Globaler Monotoniesatz ) | |
|---|---|---|
| Wenn f ' |
| Wenn f ' |
|
| Also ist nach Satz 3 die Funktion ( - f ) monoton steigend in I , also die Funktion f monoton fallend in I . |
| Ist nämlich f ' = 0 in I , so ist
f ' |
|
| Daher ist f in I monoton fallend und steigend, also konstant.
Damit ist bewiesen worden: |
| Satz 4 | Wenn f ' = 0 in I , dann ist f in I eine konstante Funktion. |
|---|
Für Anwendungen ist häufig folgende Verschärfung von Satz 3 von Interesse:
| Satz 3** | Wenn f ' > 0 in ] a | b [ , und
f ' (a) dann ist f in [ a | b ] streng monoton steigend. |
|---|
Beweis:
Zunächst folgt nach Satz 3, dass f in [ a | b ] monoton steigt.
Es sei also u < v in [ a | b ] .
Dann ist also
f (u) ![]() f (v) .
f (v) .
Wäre nun f (u) = f (v) , so wären über [ u | v ] alle
Funktionswerte mit der Ableitung f ' = 0
in [ u | v ] im Widerspruch zur Voraussetzung.
Natürlich gilt auch der zu Satz 3** duale Satz.
Beispiele:

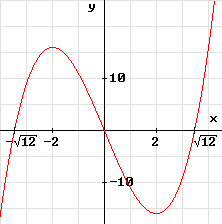
f steigt also streng monoton von - ![]() bis - 2 , fällt streng monoton zwischen
- 2 und + 2 und steigt wieder streng monoton rechts von 2 .
bis - 2 , fällt streng monoton zwischen
- 2 und + 2 und steigt wieder streng monoton rechts von 2 .
Mit diesen Ergebnissen kann man den Verlauf der Kurve skizzieren.
| f (x) = x + | 1 x |
für x > 0 hat die Ableitung | ||
| f ' (x) = 1 - | 1 x² |
. | ||
| f ' (x) < 0 in ] 0 | 1 [
|
} |
2 ist der kleinste Funktionswert |
||
| f ' (x) > 0 in ] 1 | |
||||
Die Monotoniesätze haben eine große Bedeutung, weil sie den Schluss von f ' auf f gestatten.
Die Monotoniesätze und die Beispiele legen nahe, die sog. Vorzeichenfunktion (Signum-Funktion) einzuführen.
| sign x = | { | 1 | für x > 0 | ( kurz: + ) | 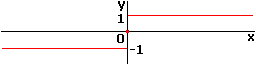 |
||||
| 0 | für x = 0 | ||||||||
| - 1 | für x < 0 | ( kurz: - ) |
" f steigt bei a und f (a) = 0 " bedeutet
" f wechselt bei a das Vorzeichen von - nach + "
und analog
f fällt bei a und f (a) = 0 ![]() f wechselt bei a das Vorzeichen von + nach - .
f wechselt bei a das Vorzeichen von + nach - .
Die Aufgabe 7 enthält in ihren beiden Teilen den Beweis des Schrankensatzes.
| Satz 5 | Schrankensatz | |
|---|---|---|
| Wenn m dann m ( v - u ) |
| m |
f (v) - f (u) v - u |
|
weiter zu
8. Anwendungen II
![]()