netSCHOOL Oberstufe: Differential- und Integralrechnung

Oberstufenskript
 Differential- und Integralrechnung
 für Grund- und Leistungskurse von Jürgen Rohde		    zurück zum INHALT
 7.2 Globale Monotoniesätze

 
8. Anwendungen II

8.1 Kurvendiskussionen

Ziel einer Kurvendikussion ist die graphische Darstellung einer Funktion. Wir stellen zunächst die erforderlichen Sätze und Definitionen zusammen.

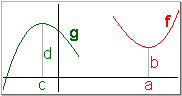
Markante Kurvenpunkte sind im nebenstehenden Bild dargestellt.
Folgende Aussagen sind jeweils gleichbedeutend:
  1. Die Funktion  f  hat bei  a  ein relatives Minimum.
  2. ( a | b ) ist Tiefpunkt
  3. f (a) = b  ist relatives Minimum.
  1. Die Funktion  g  hat bei  c  ein relatives Maximum.
  2. ( c | d ) ist Hochpunkt
  3. g (c) = d  ist relatives Maximum.
       Tiefpunkt / Hochpunkt

Definition
     ( relatives Extremum )
f  hat bei  a  ein relatives Minimum, wenn  f (a)  in einer Umgebung  U (a)  kleinster Funktionswert ist.
g  hat bei  c  ein relatives Maximum, wenn  g (c)  in einer Umgebung  U (c)  größter Funktionswert ist.
    Bemerkungen:
  1. Extremum heißt Maximum oder Minimum.
  2. Unter dem absoluten Maximum (Minimum) verstehen wir den größten (kleinsten) Funktionswert von  f  über  D .

Der Zusammenhang mit der Ableitung ist leicht zu sehen.

       Satz 1   Notwendige Bedingung für relative Extrema
Wenn  f (a)  relatives Extrema ist und  f ' (a)  existiert, dann ist  f ' (a) = 0 .
  Denn wäre  f ' (a)  0 ,
so würde  f  im Falle  f ' (a) > 0  bei  a  ansteigen und im Falle  f ' (a) < 0  bei  a  fallen
im Widerspruch zur Voraussetzung.

Zu den Begriffen "notwendige Bedingung" und "hinreichende Bedingung" beachte man die Äquivalenzen ( Äqu ) im folgenden Kasten und verdeutliche sie sich an dem Beispiel.

A : Die natürliche Zahl  n  ist durch  4  teilbar.
B : Die natürliche Zahl  n  ist durch  2  teilbar.

A B     Äqu     wenn  A , dann  B 
Äqu     aus  A  folgt  B 
Äqu     A  ist hinreichende Bedingung für  B 
Äqu     B  ist notwendige Bedingung für  A 

Beispiele:

  1. Die Funktion  f (x) = x4 - 16  hat offensichtlich bei  0  ein relatives Minimum. Es ist  f ' (0) = 0 .
  2. Für die Funktion  f  mit  f (x) = x3  ist  f ' (0) = 0  und  f  hat bei  0  kein relatives Minimum oder Maximum.   f  steigt bei  0 .
  3. Für die Funktion  f :   x | x |  ist bei  0  nicht diffenrenzierbar und hat dort ein relatives (sogar absolutes) Minimum.
Es ist sehr nützlich, diese Beispiele zu Satz 1 genau zu durchdenken (Zeichnung!).

Beispiel 2 zeigt, dass  f ' (a) = 0  nicht hinreichend ist für ein relatives Extremum. Wenn man die Bilder zu Beginn dieses Abschnitts betrachtet, erkennt man, dass bei  a  z.B. ein relatives Maximum vorliegt, wenn in  U (a)  die Funktion links von von  a  monoton steigt, rechts von  a  monoton fällt.
 
        Satz 2   1. hinreichende Bedingung für relative Extrema
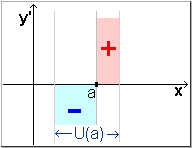
Wenn  f '  bei  a  das Vorzeichen von  +  nach  -  wechselt, dann ist  f (a)  ein relatives Maximum.
Wenn  f '  bei  a  das Vorzeichen von  -  nach  +  wechselt, dann ist  f (a)  ein relatives Minimum.

Beweis:
Monotoniesatz
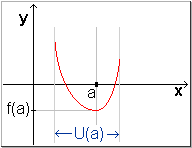f '  wechselt bei  a  das Vorzeichen von  -  nach  + 
d.h.: in einer  U (a)  ist
f ' (a)  = 0   und
f ' (x)  < 0   für   x < a   und
f ' (x)  > 0   für   a < x  .		   f  fällt links von  a  streng monoton
f  steigt rechts von  a  streng monoton
f (a)  ist kleinster Funktionswert in  U (a)  .
Der Beweis ergibt sich für ein relatives Minimum aus den Bildern, den Erläuterungen dazu und aus dem Monotoniesatz.
Der Beweis für ein relatives Maximum ist als Aufgabe durchzuführen.

Beispiele:

  1. y = 2 x³ - 3 x² - 36 x + 16   hat die Ableitung   y ' = 6 x² - 6 x - 36   mit den Nullstellen  ( -2 )  und  3 . Beide sind einfache Nullstellen, also wechselt  y '  bei  ( -2 )  und  3  das Vorzeichen und  y  hat hier Extrema, und zwar ist  ( -2 | 60 )  relatives Maximum und  ( 3 | -65 )  relatives Minimum.
  2. Die Ableitung einer Funktion  f  sei   f ' (x) = ( x - 3 ) ( x + 2 )² ( x + 1 )³ 
    f '  wechselt das Vorzeichen bei  3  und  ( -1 ) , nicht bei  ( -2 ) .
    Tabelle zur Ermittlung des Vorzeichenwechsels:
        x-Achse
    sign ( x - 3 ) 
    sign ( x + 2 )² 
    sign ( x + 1 )³ 
    sign f ' (x) 
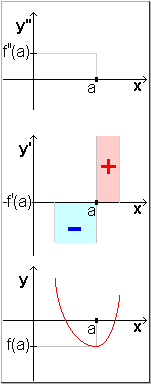    Also hat  f  bei  ( -1 )  ein relatives Maximum und bei  3  ein relatives Minimum.
    Bei  ( -2 )  hat  f  eine horizontale Tangente, Satz ist aber nicht anwendbar, denn bei  ( -2 )  hat  f '  keinen Vorzeichenwechsel.
 
Wenn man die 2. Ableitung  f "  (das ist die Ableitung von  f ' ) von  f  kennt und diese von Null verschieden ist, gelangt man leicht zu einer weniger allgemeinen, aber noch einfacher zu handhabender hinreichenden Bedingung für Extrema.

Ist nämlich  f ' (a) = 0 
und  f " (a)  0 ,   z.B.  f " (a) > 0 ,
so ist nach dem lokalen Monotoniesatz  a  eine Steigstelle von  f ' .
Wegen  f ' (a) = 0  folgt hieraus, dass  f '  bei  a  das Vorzeichen von  -  nach  +  wechselt. Also ist  f (a)  relatives Minimum.

Wir haben also damit bewiesen

       Satz 3       2. hinreichende Bedingung für relative Extrema    
Wenn  f ' (a) = 0  und  f " (a) > 0  ist,
ist  f (a)  relatives Minimum.

Wenn  f ' (a) = 0  und  f " (a) < 0  ist,
dann ist  f (a)  relatives Maximum

Beispiele:

  1. In Beispiel 4. ist  y ' = 6 x² - 6 x - 36  mit den Nullstellen  ( -2 )  und  3 .
    Wegen    y "  = 12 x - 6
    ist     y " (-2) = -30    und    y " (3) = 30 .
    Weil  y ' (-2) = 0 und  y " (-2) < 0  ist, ist  ( -2 | 60 )  relatives Maximum.
    Weil  y ' (3) = 0 und  y " (3) > 0  ist, ist  ( 3 | -65 )  relatives Minimum.
  2. Wenn  y = x4 - 16 , dann ist  y ' = 4 x³ ;  y " = 12 x² .
    Also ist  y ' (0) = 0  und  y " (0) = 0 . Satz 3 ist nicht anwendbar. Wohl aber Satz 2, denn
     y ' = 4 x³  hat bei  0  einen Vorzeichenwechsel von  -  nach  + , also ist  ( 0 | -16 )  Tiefpunkt von  y = x4 - 16 .

weiter zu    8.1 Kurvendiskussionen Satz 4  

 zurück zu MATHEMATIK Übersicht