Oberstufe: Differential- und Integralrechnung

Oberstufenskript Differential- und Integralrechnung für Grund- und Leistungskurse von Jürgen Rohde

zurück zum INHALT

 8.1 Kurvendiskussion

 
In den Übungsaufgaben wird bewiesen:

	Satz 4	3. hinreichende Bedingung für relative Extrema
		Wenn für eine gerade Zahl  n  f ' (a) = f '' (a) = f ''' (a) = . . . = f (n-1) (a) = 0  und  f (n) < 0  ( bzw.  f (n) > 0 ) dann ist  f (a)  relatives Maximum ( bzw. Minimum ).
		Bemerkungen:  f (n)  bedeutet  n-te Ableitung von  f .  f (n) = ( f (n-1) ) '     ( rekursive Definition )

Beispiel:

8.	Im Beispiel 7.    x x4 - 16      ( y = x4 - 16 ) ist  y ' (0) = 0 =  y '' (0) =  y ''' (0)   und  y (4) = 24  >  0 , also ist  ( 0 | -16 )  nach Satz 4 Tiefpunkt.

Die 2. Ableitung ist überhaupt bedeutsam für die gegeseitige Lage von Kurve und Tangente. Es gilt nämlich:

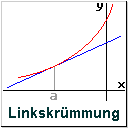
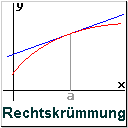
	Satz 5	Wenn  f '' (a)  >  0  ist, dann liegt in einer  U (a)  die Kurve der Funktion  f  über der Tangente durch  ( a | f (a) ) . Wenn  f '' (a)  <  0  ist, dann liegt in einer  U (a)  die Kurve der Funktion  f  unter der Tangente durch  ( a | f (a) ) .

Der Beweis folgt aus dem Schrankensatz (Satz 5 in 7.2 Globale Monotoniesätze).
Denn ist z.B.  f '' (a)  >  0 , so steigt  f '  bei  a .

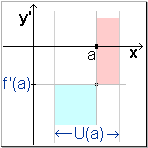		Es gibt eine Umgebung um  a , worüber für
		x < a			x > a
		f ' (x) <	f ' (a)		f ' (x) >	f ' (a)
		f (a) - f (x)	f ' (a) ( a - x )		f (a) - f (x)	f ' (a) ( a - x )
		f (x)	f (a) + f ' (a) ( a - x )		f (x)	f (a) + f ' (a) ( a - x )

Analog schließt man im Falle  f '' (a)  <  0  (Aufgabe).

Von besonderem Interesse ist der Fall, dass die Funktion  f ''  bei  a  einen Vorzeichenwechsel hat, z.B. von  +  nach  - . Dann hat die Funktion  f '  bei  a  sicher ein relatives Maximum.
In einer  U (a)  folgt genauer für

x < a			x > a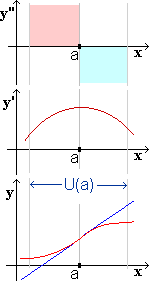
f '' (x)  >	0		f '' (x)  <	0
			globaler Monotoniesatz
f ' (x)  <	f ' (a)		f ' (x)  <	f ' (a)
			Schrankensatz
f (a) - f (x)	f ' (a) ( a - x )		f (x) - f (a)	f ' (a) ( x - a )
f (x)	f (a) + f ' (a) ( a - x )		f (x)	f (a) + f ' (a) ( x - a )
Also liegt die Kurve der Funktion  f
über der Tangente			unter der Tangente
durch  ( a | f (a) )
Die Kurve  f  wendet also im Punkt  ( a | f (a) ) von einer Seite der Tangente zur anderen. ( a | f (a) )  heißt Wendepunkt.

Wir haben bewiesen

	Satz 6	1. hinreichende Bedingung für Wendepunkte
		Wenn  f ''  bei  a  das Vorzeichen wechselt, dann ist  a  Wendestelle von  f . [ ( a | f (a) )  Wendepunkt ]

Weitgehend analog zur Lösung von Extremwertproblemen gelten und beweist man folgende Sätze ( vergleiche Aufgaben ):

	Satz 7	2. hinreichende Bedingung für Wendepunkte
		Wenn  f '' (a) = 0  und  f ''' (a) 0  ist, dann ist  a  Wendestelle von  f .

	Satz 8	3. hinreichende Bedingung für Wendepunkte
		Wenn  f '' (a) = 0 =  f ''' (a) = . . . = f (n-1) (a)  und  f (n) 0  für eine ungerade Zahl n 3 , dann ist  a  Wendestelle von  f .

	Satz 9	notwendige Bedingung für Wendepunkte
		Wenn  a  Wendestelle von  f  ist und  f '' (a) existiert, dann ist  f '' (a) = 0 .

 
Beispiele:

9.	Die Funktion  F :  x x³  hat den Ursprung als Wendepunkt. Die  x-Achse ist Wendetangente. Es ist  f '' (0) = 0. Satz 9 ist bestätigt.
10.	Jede ganzrationale Funktion 3. Grades hat genau einen Wendepunkt.
	Denn ist	f (x) = a x³ + b x² + c x + d ,
	so ist	f '' (x) = 6 a x + 2 b
	mit der Nullstelle  ( -b/3a ) . Da außerdem  f ''' (x) = 6 a   0  ist, hat  f  bei  ( -b/3a )  nach Satz 7 einen Wendepunkt. Selbstverständlich folgt dies auch aus Satz 6 .
11.	Es sei	f (x) = ( x - 1 )5 ( x + 2 )
	1  ist dreifache Nullstelle von  f '' . Also wechselt  f ''  bei  1  das Vorzeichen und folglich hat  f  bei  1  einen Wendepunkt.
	Oder zur Kontrolle	y ' = 3 ( x - 1 )4 ( 2 x + 3 )  y '' = 30 ( x - 1 )³ ( x + 1 )  y ''' = 60 ( x - 1 )² ( 2 x + 1 )  y '' (1) = 0  und Vorzeichenwechsel  ( 1 | 0 )  Wendepunkt;  y (5) (1)  0

weiter zu    12. Beispiel einer Kurvendiskussion  

 zurück zu MATHEMATIK Übersicht