netSCHOOL AUFGABEN zu Differential-/Integralrechnung
[  I N H A L T  ]     [ MATHEMATIK Übersicht ]

Aufgaben zu
8. Anwendungen II
 
8.1 Kurvendiskussionen

1. Zeige, dass keine der Voraussetzungen in Satz 1 überflüssig ist.
2. Zeige, dass die Umkehrung von Satz 1 falsch ist.
3. Beweise Teil 1 des Satzes 2 im einzelnen (mit Zeichnungen).
4. Erkläre, warum Satz 2 allgemeiner ist als Satz 3. Erläutere auch an einem Beispiel.
5. Beweise Satz 4.
6. Beweise Satz 5 für den Fall  f '' (a)  <  0 .
7. Beweise   a) Satz 7,   b) Satz 8,   c) Satz 9,   d) Satz 6
8. Wir geben zunächst eine Definition:
Definition: Die Funktion  f  heißt an der Stelle  a  linksgekrümmt, wenn die Funktion  f '  bei  a  steigt (Bild links).
links herum und rechts herum
  1. Definiere " f  heißt bei  a  rechtsgekrümmt" (Bild rechts).
  2. Beweise:
    Wenn  f '' (a)  >  0 , dann ist  f  bei  a  linksgekrümmt.
    Wenn  f '' (a)  <  0 , dann ist  f  bei  a  rechtsgekrümmt.
    (Anleitung: beachte den lokalen Monotoniesatz und dass  f ''  die Ableitung von  f '  ist.)
  3. Beweise: (vergleiche den Beweis zu Satz 5)
    Wenn  f  bei  a  linksgekrümmt ist, dann liegt  f  in einer  U (a)  über der Tangente durch  ( a | f (a) ) . Wie lautet die Gleichung der Tangente?
  4. Formuliere und beweise den zu Satz Aufgabe 8c dualen Satz.
  5. Definiere den Begriff des Wendepunktes unter Benutzung des Krümmungsbegriffs und zeige die Gleichwertigkeit mit der bereits bekannten Definition.
9. Zeige:  f (x)  = x · | x |  hat bei  0  eine Wendestelle, aber  f '' (0)  existiert nicht. Was bedeutet dies Beispiel für Satz 9?
10. Gib ein Beispiel dafür an, dass  g '' (x)  = 0  keine hinreichende Bedingung für eine Wendestelle der Funktion  g  ist.
11. Warum hat  x 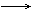 1/x²  bei  0  keine Wendestelle?
12. Begründe, warum nach Satz 6 und nach Satz 8 die Funktion  x 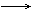 x9  im Ursprung einen Wendepunkt hat. Warum folgt dies nicht aus Satz 7 ?
13. Was folgt aus . . . ?
  1. f ' (3) = 4
  2. f ' (2) = -1
  3. f ' (1) = 0
  4. f '' (2) = 0
  5. f ' (4) = 0  und  f '' (4) = 5
  6. f ' (-2) = 0  und  f '' (-2) = -20
  7. f ' (2) = 4  und  f '' (2) = 0  und  f ''' (2) = 5  und  f (2) = 1
  8. f (-1) = 3 und  f ' (-1) = -4  und  f '' (-1) = 0  und  f ''' (-1) = -10 
  9. f (-3) = 4 und  f ' (-3) = 0  und  f '' (-3) = 0  und  f ''' (-3) = 40 
  10. f ' (3) > 0  und  f '' (3) < 0
  11. f ' (3) < 0  und  f '' (3) > 0
14. Wo liegen die relative Extrema der Funktion  f , wenn die Funktion  f '  gegeben ist durch: . . . ?
  1. f ' (x)  =  -2 · ( x - 4 )³ · ( x + 2 )² · ( x + 0,1)
  2. f ' (x)  =  ( x² - 1 ) · ( x² - 4 )³ · ( x² - y )²
  3. f ' (x)  =  ( x + 1 ) · g (x)  mit  g (-1) 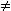 0 ;  g  ganzrationale Funktion
  4. f ' (x)  =  ( x + 1 )² · g (x)  mit  g (-1) 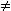 0 ;  g  ganzrationale Funktion
15. Wo liegen die Wendepunkte der Funktion  f , wenn die Funktion  f ''  gegeben ist durch
  1. f ''  =  ( x + 3 ) · ( x - 2 )² · ( x + 1 )5
  2. f ''  =  x² + 2 x - 3
16. Diskutiere wie Beispiel 12
  1. y = x³ - 12 x
  2. y = x³ - 2 x²
  3. y = 2 x4 - ½ x2
  4. y = 2 x5 - 3 x2
  5. y = 1/5 x5 - 2 x3 + 5 x
  6. y = 2 x³ - 15 x² + 36 x + 24
  7. y = x³ + 2 x² - x - 2
  8. y = x³ - 2 x² - 2 x + 1
  9. y = 2 x4 - 4 x3 + 4 x - 2
  10. y = x³ - 9 x - 8
  11. y = x³ - 6 x² + 12 x - 8
  12. y = x³ + 3 x² - 9 x - 3
  13. y = 9 x - x²
  14. y = x³ - 5 x² + 3 x
  15. y = 4 x3 - x4
  16. y = ( x - 1 ) · ( x + 1 )²
  17. y = 2 x³ - 9 x² + 12
  18. y = x² - 1/6 x³
  19. y = x4 - 2 x2
  20. y = x4 - 6 x2 + 5
  21. y = 1/18 x4 - x2 + 11/2
  22. y = 20 x3 - 3 x5

 

weitere Aufgaben zu    8.2 Bestimmung von Funktionsgleichungen  

 zurück zu MATHEMATIK Übersicht