 |
Oberstufe: Differential- und Integralrechnung
|
Oberstufenskript
Differential- und Integralrechnung
für Grund- und Leistungskurse von Jürgen Rohde |
|
 zurück zum INHALT
zurück zum INHALT |
 8.1 Kurvendiskussion
8.1 Kurvendiskussion
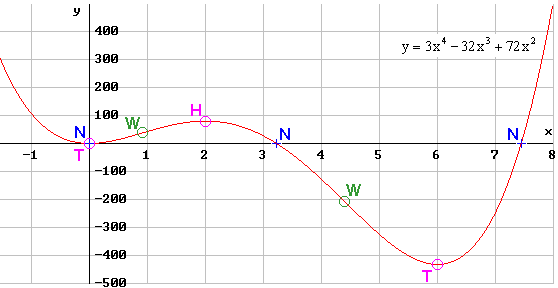
12. Beispiel einer Kurvendiskussion
Diskutiere und zeichne die Kurve der Funkion f mit
f (x) = 3 x 4 - 32 x3 + 72 x2
Lösung:
- Maximaler Definitionsbereich:
 (wie bei allen ganzrationalen Funktionen)
(wie bei allen ganzrationalen Funktionen)
- Symetrien: hier keine erkennbar
- Nullstellen:
3 x 4 - 32 x³ + 72 x² = 0
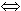 x² ( 3 x² - 32 x + 72 )
x² ( 3 x² - 32 x + 72 )
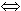 x = 0 oder
x² - 32/3 x + 24 = 0
x = 0 oder
x² - 32/3 x + 24 = 0
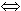 x = 0 oder
x
x = 0 oder
x 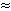 7,44 oder
x
7,44 oder
x 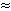 3,23
3,23
- Ableitungen:
f ' (x) = 12 x³ - 96 x² + 144 x
f '' (x) = 36 x² - 192 x + 144
f ''' (x) = 72 x - 192
- Relative Extrema:
Notwendige Bedingung: f ' (x) = 0
12 x³ - 96 x² + 144 x = 0
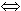 x = 0 oder x = 2 oder x = 6
x = 0 oder x = 2 oder x = 6
Also können bei 0 ; 2 ; 6 relative Extrema vorhanden sein.
f ' (0) = 0 und f '' (0) = 144 > 0
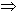 ( 0 | 0 ) ist Tiefpunkt
( 0 | 0 ) ist Tiefpunkt
f ' (2) = 0 und f '' (2) = -96 < 0
 ( 2 | 80 ) ist Hochpunkt
( 2 | 80 ) ist Hochpunkt
f ' (6) = 0 und f '' (6) = 288 > 0
 ( 6 | -432 ) ist Tiefpunkt
( 6 | -432 ) ist Tiefpunkt
- Die Nullstellen von f '' können Wendestellen sein.
36 x² - 192 x + 144 = 0
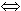 x² - 16/3 x + 4 = 0
x² - 16/3 x + 4 = 0
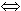 x
x 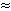 2,67 ± 1,76
2,67 ± 1,76
x 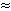 4,43 oder
x
4,43 oder
x 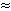 0,90
0,90
- Wegen
3 x 4 - 32 x³ + 72 x² =
x4 ( 3 - 32/x + 72/x² )
überschreiten die Funktionswerte für x
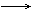
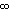 und für x
und für x
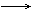 -
- 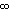 jede positive reele Zahl.
jede positive reele Zahl.
Also ist der Wertebereich
{ x 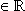 | x
| x 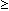 -432 }
-432 }
- Tabelle einiger nützlicher Funktionwerte (zusätzlich)
| x |
-1 | -2 | -½ |
8 | 9 | 1 |
| y |
107 | 592 | 22,19 |
512 | 2187 | 43 |
- Darstellung der Kurve der Funktion f
Aufgaben zu 8.1
weiter zu
8.2 Bestimmung von Funktionsgleichungen
 zurück zu MATHEMATIK Übersicht
zurück zu MATHEMATIK Übersicht

![]()