netSCHOOL Oberstufe: Differential- und Integralrechnung

Oberstufenskript
 Differential- und Integralrechnung
 für Grund- und Leistungskurse von Jürgen Rohde		    zurück zum INHALT
 6. Anwendungen I

 
7. Monotoniesätze

7.1 Lokale Monotoniesätze

In diesem Paragraphen werden die Zusammenhänge der Ableitung an einer Stelle und das Steigungsverhalten der Funktion an dieser Stelle untersucht.
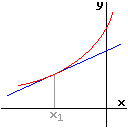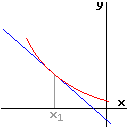      steigend       fallend
       m > 0 ;  f  steigend bei  x1         m < 0 ;  f  fallend bei  x1 

Die Bilder geben einen ersten anschaulichen Einblick.

Hier zunächst die Definition für steigend und fallend:

      Die Funktion  f  steigt bei  x0 , wenn in einer Umgebung um  x0 
 f (x) < f (x0) für  x < x0  und
 f (x) > f (x0) für  x > x0  ist.
Die Funktion  f  fällt bei  x0 , wenn in einer U (x0)
 f (x) > f (x0) für  x < x0  und
 f (x) < f (x0) für  x > x0  ist.

Wenn  f ' (x1)  existiert, so gibt es definitionsgemäß (Definition der L-Differenzierbarkeit) eine Zahl  k > 0 , so dass in einer  U (x1)  die Ungleichungskette gilt:
 
 D   f (x1) + f ' (x1) · ( x - x1 ) - k ( x - x1 )²   f (x) f (x1) + f ' (x1) · ( x - x1 ) + k ( x - x1 )²
P-   f (x) P+

Die linken und rechten Terme von  D  sind quadratische Funktionen von  x . Ihre Bilder sind also Parabeln. P- ist nach unten, P+ nach oben geöffnet. Die Funktionen  f ,  P-  und  P+  gehen durch den Punkt ( x1 | f (x1) ) und haben in diesem Punkt eine gemeinsame Tangente mit dem Tangententerm   f (x1) + f ' (x1) · ( x - x1 ) .

Steigung > 0 Bild 1
 
Steigung < 0

 

 

 

 
 

Bild 2


Die Kurve der Funktion  f  verläuft in einer  U (x1)  zwischen den beiden Parabeln  P+  und  P-  in dem durch Grautönung angedeuteten Bereich. Man nennt den zwischen den Parabeln liegenden Bereich der  x-y-Ebene  einen Parabelsektor.
Dann gilt nach  D  (vergleiche Bild 1 und Bild 2):

       Satz 1  (Geometrische Charakterisierung der Diffenerenzierbarkeit)
  f ' (x1) existiert     Es gibt einen Parabelsektor durch ( x1 | f (x1) ) ,
welcher die Kurve von  f  über einer  U (x1)  verdeckt.
 
 Anmerkung:  Es gibt - falls überhaupt - beliebig viele verdeckende Parabelsektoren,
denn wenn einer die Kurve bei  x1  verdeckt, dann tut es auch jeder "breitere" mit größerem  k .

Die Monotonieaussagen werden nun präzisiert.
Aus Bild 1 in Verbindung mit  D  (siehe oben) liest man ab:

      Es ist   f (x) < f (x1) ,  wenn x   ] x1 - 1
k		 f ' (x1) | x1 [
und f (x) > f (x1) ,  wenn x   ] x1 | x1 + 1
k		 f ' (x1) [
Analoges liest man aus Bild 2 ab. Also gilt
 
  Satz 2   (Lokaler Monotoniesatz)
Wenn f ' (x1) > 0 ist,     dann steigt  f  bei  x1  .
Wenn f ' (x1) < 0 ist,     dann fällt  f  bei  x1  .

 

weiter zu    7.2 Globale Monotoniesätze  

 zurück zu MATHEMATIK Übersicht