Oberstufe: Differential- und Integralrechnung

Oberstufenskript Differential- und Integralrechnung für Grund- und Leistungskurse von Jürgen Rohde

zurück zum INHALT

 5.4 Die Ableitung einiger spezieller nicht ganzrationaler Funktionen

 
6. Anwendungen I

 
Beispiele

1. Wie lautet die Gleichung der Tangente an der Kurve zu  y = x³ + 4 x² - 6 x + 5   an der Stelle  2 ?

   Lösung:	y (2)	= 8 + 4 · 4 - 6 · 2 + 5 = 17
   	y '	= 3 x² + 8 x - 6
   	y ' (2)	= 3 · 4 + 8 · 2 - 6 = 22
   	Gleichung der Tangente: y = 17 + 22 ( x - 2 ) = 22 x - 27

2. Wie lauten die Gleichungen der Tangenten an die Parabel  y = x²  vom Punkt ( 1 | -1 ) aus?

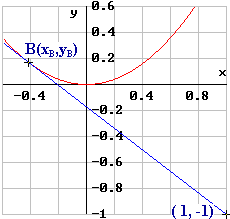   		Lösung: Im Bild ist nur eine Lösung angedeutet. B liegt
   		1.	auf der Parabel, also
   			yB = xB² ,	(1)
   		2.	auf einer Tangente mit der Gleichung y = - 1 + 2 xB ( x - 1 ) , also
   			yB = - 1 + 2 xB ( xB - 1 ) .	(2)

   
   

   Aus (1) und (2) folgt durch Gleichsetzung
   xB² = - 1 + 2 xB² - 2 xB		xB² - 2 xB - 1 = 0
   mit den beiden Lösungen  xB = 2,414 und xB = - 0,414 . Also gibt es zwei Tangenten mit den Gleichungen
   y = - 1 + 4,828 ( x - 1 )	bzw.	y = - 1 - 0,828 ( x - 1 )

3. Berechne näherungsweise

   a.	( 0,996 )5		b.	( 2,04 )6
   Lösung a.	Der Tangententerm an der Stelle  1  der Funktion  x x5  lautet
   	t (x) = 1 + 5 ( x - 1 )		( 0,996 )5 =	( 1 - 0,004 )5 1 - 5 · 0,004 = 0,98
   Lösung b.	Analog:
   	( 2 + 0,04 )6		64 + 6 · 0,04 · 25 = 71,68

4. Berechne näherungsweise eine Nullstelle von  f (x) = x³ - x + 1  . Eine Wertetabelle läßt eine Lösung zwischen ( -2 ) und ( -1 ) vermuten. Man kann auch graphisch eine erste Näherung für die Nullstelle finden.
   (1)    x³ - x + 1 = 0     x³ = x - 1
   Also sind die Lösungen von (1) zugleich die x-Werte der Schnittpunkte der beiden Kurven y = x³ und y = x - 1 .
   

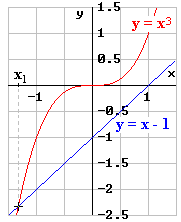   Zur Bestimmung einer 1. Näherung x1

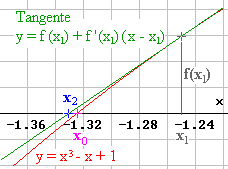   Bild zum Näherungsverfahren

   
   Es sei  x₁ = 1¼ = 1,25 gewählt (hier rechnet man absichtlich mit Brüchen). Es soll eine bessere Näherung für  x₀  gefunden werden.
   Dazu ersetzt man die Kurve bei  x₁  durch die Tangente an die Kurve im Punkt ( x₁ | f (x₁) ) und wählt den Schnittpunkt  x₂  der Tangente mit der x-Achse als 2. Näherung für  x₀ .
   Da  f (x₁) = 19/64  und  f ' (x₁) = 59/16  ist, lautet die Tangentengleichung

   y = 19/64 + 59/16 ( x + 5/4 )     x₂ = - 5/4 - 19/64 · 16/59 = - 157/118 - 1,33

   Man setzt  x₂ = - 4/3  und wiederholt das Verfahren.
   Das Hornerschema kann hier gut eingesetzt werden.

   Man erhält  f (-4/3) = - 1/27 ;      f ' (-4/3) = 13/3       x₃ = -155/117 - 1,3248

   Durch Probe wird bestätigt:   x₀ [ - 1,3247 | - 1,3248 ] .
   Die Existenz der Nullstelle wird hier nicht problematisiert. Es wird auch erst später gezeigt, dass das sog. Newtonsche Näherungsverfahren "beliebig gute" Lösungen liefert.

5. Ein Körper werde vom Erdboden senkrecht nach oben geschossen.
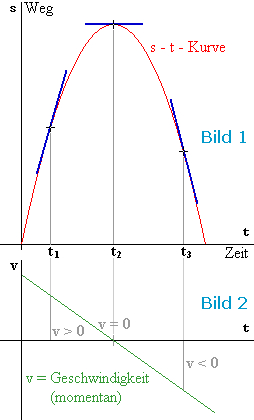   Zu jedem Zeitpunkt  t  werde die Höhe des Körpers über dem Erdboden registriert.
   Ergebnis siehe Bild 1.
   Nun möchte man z.B. die Geschwindigkeit des Körpers zur Zeit  t₁  wissen.

   Der "naive" Geschwindigkeitsbegriff	Wegänderung	=	s
   	Zeitänderung		t

   
   bezieht sich auf ein Zeitintervall. Geschwindigkeit zu einem Zeitpunkt muss erst noch definiert werden.

   Dazu folgender Gedankengang:
   Das Bild einer gleichförmig geradlinigen Bewegung in einem s-t-Diagramm ist eine Gerade. Ihre Steigung ist definitionsgemäß die (konstante) Geschwindigkeit der Bewegung. Es liegt nun nahe, die s-t-Kurve in Bild 1 zu bestimmten Zeitpunkten durch lineare Funktionen zu approximieren.
   Es entsprechen sich (vergleiche Bild 1 ):
   

   mathematisch	physikalisch
   lineare Funktion Tangente Ableitung = Tangentensteigung	gleichförmige Bewegung lineare Approx. durch gleichf. Bewegung Momentangeschwindigkeit

   In  t₁  ist die Momentangeschwindigkeit  v  positiv, d.h. der Körper entfernt sich von der Erde.
   In  t₂  ist  v = 0  (Umkehrpunkt)
   In  t₃  ist  v < 0  . Der Körper kehrt momentan zur Erde zurück. Vergleiche Bild 2

Aufgaben zu 6.  

weiter zu    7. Monotoniesätze  

 zurück zu MATHEMATIK Übersicht