| AUFGABEN zu Differential-/Integralrechnung |
| [ I N H A L T ] | [ MATHEMATIK Übersicht ] |
| 1. | Bestimme die Gleichung der Tangente an die Kurve der Funktion f an der Stelle x1 . | |||
| a) | f (x) = x³ - 2 x + 1 | x1 = 2 ; x1 = - 1 | ||
| b) | f (x) = - 3 x4 + 5 x² - 16 | x1 = 0,5 | ||
| c) | f (x) = 3 - x² | x1 = 3 ; x1 = - 3 | ||
| d) | f (x) = 2 x² + x³ | x1 = 4 | ||
| 2. | Wo schneidet die Tangente an die Kurve y = x³ an der Stelle 4 die Kurve (neben x = 4 ) ein zweites Mal? | |||
| 3. | Wie lauten die Gleichungen der Tangenten, die man von | |||
| a) | ( - 2 | 3 ) | b) | ( 2 | 3 ) | |
| aus an die Parabel y = x² ziehen kann? | ||||
| 4. | Gegeben sei die Normalparabel y = x² | 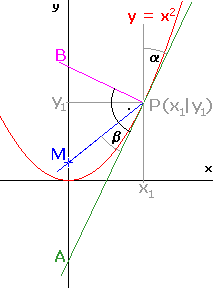
| |
| a) | Zeige: A = ( 0 | - y1 ) | ||
| b) | BP senkrecht zu Parabel in P .
Zeige: B = ( 0 | y1 + ½ ) |
||
| c) | Warum liegen die Punkte A B P auf einem Thaleskreis ?
Bestätige: Mittelpunkt M des Thaleskreises: M ( 0 | ¼ ) . Also hängt M nicht von x1 ab. |
||
| d) | Beweise: Die beiden eingezeichneten Winkel (Alpha, Betha) sind gleich. | ||
| e) | Man deute die Parabel als Achsenschnitt durch einen Parabolspiegel und zeige: Alle Lichtstrahlen, die parallel zur (optischen) Achse einfallen, werden durch M reflektiert. M = Brennpunkt. Anwendung: Parabolspiegel, Radarantenne, Satelitenschüssel. | ||
| f) | Zeige: Für alle Punkte der Parabel gilt: Ihr Abstand von M ist gleich ihrem Abstand von der Geraden y = ¼ . Diese Gerade heißt Leitlinie der Parabel. | ||
| 5. | Übertrage die Ergebnisse von 4. auf die Parabeln y = a · x² . |
| 6. | Zeige, dass y = | x |³ nicht die Brennpunkteigenschaft 4e) hat. |
| 7. | Berechne näherungsweise: | 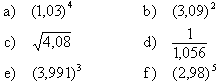 |
| 8. | Begründe die Näherungsformeln für kleine |x|: | 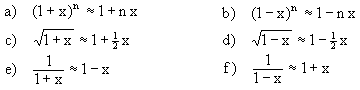 |
| 9. | Berechne näherungsweise die Nullstellen der folgenden Funktionen. Die Ungenauigkeit sei kleiner als 10-3. Benutze Taschenrechner und Hornerschema. | |||
| a) | f (x) = 2 x² - 3 x + 1 + x³ | b) | f (x) = x³ - 3 x² + 6 x - 9 | |
| c) | f (x) = x³ - 7 | d) | f (x) = x5 - 3 | |
| e) | f (x) = 2 x5 - 4 x4 + 5 x³ - 2 x² + x - 5 | f) | f (x) = 4 x4 - 3 x² - 8 x - 2 | |
| g) | f (x) = x4 + 3 x³ + x² - 2 x - 1 | h) | f (x) = 4 x³ + 12 x² + 8 x - 1 | |
| i) | f (x) = x5 + 17,12 | k) | f (x) = x³ + x - 1 | |
| 10. | Ein senkrecht nach oben geworfenenr Körper bewegt sich nach dem Weg-Zeit-Gesetz s (t) = 4 t - 5 t² . Dabei steht t für die in Sekunden gemessene Zeit. | |
| a) | Wie groß ist die Momentangeschwindigkeit
zur Zeit: t1 = 0 ; t2 = 0,1 ; t3 = 0,4 ; t4 = 0,8 ? |
|
| b) | Wann kehrt der Körper um? | |
| c) | Wann kehrt der Körper zurück? | |
| d) | Wie heißt das Geschwindigkeits-Zeit Gesetz? | |
| 11. | Es sei s (t) = 2 t³ - t² + 4 t - 5 . Bestimme v (t) . Wann ist v (t) = 0 ? |
| 12. | Berechne die Stellen mit horizontaler Tangente bei | ||||||
| a) | y = 3/5 x5 - 13 x³ + 96 x - 17 | b) | y = x5 - 65/3 x³ + 180 x | c) | y = ( 2 x - 1 )² · ( 2 x + 1 )³ | ||
| 13. | Zeige: Die Gerade x + 4 y - 5 = 0 ist Normale zu y = x² + 2 x - 2 . |
| 14. | Bestimme a so, dass die Kurve y = a x³ die Gerade y = 6 x + 4 berührt. |
weitere Aufgaben zu
7. Monotoniesätze
![]()