Oberstufe: Differential- und Integralrechnung

Oberstufenskript Differential- und Integralrechnung für Grund- und Leistungskurse von Jürgen Rohde

zurück zum INHALT

 4.7 Interpolation durch ganzrationale Funktionen

 
5. Lineare Approximation

Zur Wiederholung, aber auch zur Vereinheitlichung der Begriffsbildung sei folgendes vorausgeschickt:

5.1 Allgemeines zum Funktionsbegriff

Jede Zuordnung, welche den Zahlen  x  einer Definitionsmenge  D  eindeutig eine reelle Zahl  f (x)  zuordnet, heißt (reelle) Funktion.

	D		bedeutet " f  bildet D eindeutig in ab ".
	x		f (x) bedeutet " der Zahl  x  wird die Zahl  f (x)  zugeordnet ".
Funktionen lassen sich auch als Maschinen deuten.
	x		f (x)
Die f-Maschine erzeugt aus der Eingabe  x  die Ausgabe  f (x) .
f (D)  = W = { f (x) | x D } heißt Wertemenge von  f .
f (x)  heißt Funktionsterm, gelegentlich auch Funktionswert von x .

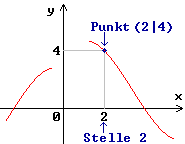Wenn z.B. 2 D, dann heißt f (2) (gelesen: f von 2 ) Funktionswert an der Stelle 2 .

Die Menge aller Punkte ( x | f (x) )   ( x D ) in einem kartesischen Koordinatensystem heißt Graph oder Kurve der Funktion f ; übrigens auch dann, wenn sie aus einzelnen Punkten oder den Punkten einer Geraden besteht. Funktionskurven liegen wegen der Eindeutigkeitsbedingung "schlicht" über der x-Achse, d.h. jede Parallele zur y-Achse hat mit der Kurve höchstens einen Punkt gemeinsam.
 
Gleichungen wie
        f (x) = x² - 7   oder   y = x³ - 7
heißen Funktionsgleichungen, denn jedem  x  (hier aus ) ist durch den Funktionsterm auf der rechten Seite der Gleichung genau ein  f (x)  bzw. y zugeordnet. Die Lösungsmenge von
        y = x³ - 7
ist eine Funktionskurve.

Allgemein ist jede Gleichung
        F ( x | y ) = 0
in den Variablen  x  und  y  eine Funktionsgleichung, wenn zu jedem x  höchstens ein Paar ( x | y ) zur Lösungsmenge gehört.

Z.B. ist die Gleichung
(1)     x² + y² - r² = 0
eines Kreises um den Ursprung mit dem Radius  r  keine Funktionsgleichung: ( 0 | r ) und ( 0 | -r ) erfüllen (1).
Allerdings kann man (1) in zwei Funktionsgleichungen aufspalten:
(2)     y =  und  y = -

Dagegen ist
(3)     x² · y - y - x² = 0
eine Funktionsgleichung.

(2) ist nicht für alle x  definiert. Es gibt eine maximale Definitionsmenge, nämlich [ -r | +r ].
Die maximale Definitionsmenge von (3) ist \ { -1, 1 } .

 
5.2 Der Grundgedanke der linearen Approximation

Grundidee der Differenzialrechnung ist die Approximation (Annäherung) möglichst beliebiger Funktionen wenigstens in der Umgebung einer Stelle durch lineare Funkionen.

Unter einer Umgebung um  x₀  - in Zeichen  U (x₀) - verstehen wir jedes offene Intervall, in dem  x₀  liegt.
Der Index  0  bei  x₀  soll anzeigen, dass  x₀  während der folgenden Betrachtungen eine feste reelle Zahl sein soll.

Zur Mathematisierung der Grundidee liegt der Ansatz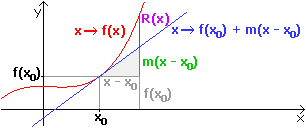
	(1)	f (x) = f (x0) + m ( x - x0 ) + R (x)
über  U (x0) D  nahe.

x f (x₀) + m ( x - x₀ )   ist jedenfalls eine lineare Funktion durch ( x₀ | f (x₀) ) .
R (x) ist durch die Gleichung (1) definiert und gibt den Unterschied (Differenz) der Funktionswerte der linearen Funktion
x f (x₀) + m ( x - x₀ )   und der Funktion  f  über U (x₀) in Abhängigkeit von  x  an. Im Hinblick auf die angestrebte Approximation sind für  R (x)  die Bezeichnungen "Ungenauigkeit", "Rest" oder "Fehler" anschaulich. Es ist plausibel, dass | R (x) | insbesondere für x-Werte sehr nahe bei  x₀  sehr klein werden soll und dass | R (x) | um so größer ausfallen kann, je größer der Abstand | x - x₀ | von  x  und  x₀  ist.

Man könnte naheliegenderweise
	(2)	| R (x) | k · | x - x0 |µ      über U (x0)
probieren mit einer positiven reellen Zahl  k  und  µ > 0 . Für  µ = 1 , d.h. für
		| R (x) | k · | x - x0 |

zeigt man leicht, dass  m  in (1) keineswegs eindeutig bestimmt ist, was sicher niemand akzeptieren möchte.
Es sollte also schon  µ > 1   sein.
Dann ist  m  eindeutig bestimmt und der Ansatz möglich und nachdenkenswert. Wir würden allerdings der Einfachheit halber nicht beliebige  µ  zulassen, sondern ein ganzzahliges  µ  vorziehen.  µ = 3 oder größer ist aber wenig sinnvoll, weil dann die Quadratische Funktion  y = x²  wegen  | x - x₀ |² > | x - x₀ |³  für  | x - x₀ | < 1  nirgends linear approximierbar wäre, was sicher ein unvernünftiges Ergebnis wäre.

Wir entscheiden uns daher für  µ = 2  und definieren:
 

	Die Funktion  f  heißt an der Stelle  x0  L-differenzierbar, wenn es eine Zahl  m  gibt, so dass das durch die Gleichung
	(1)	f (x) = f (x0) + m ( x - x0 ) + R (x)
	definierte Restglied  R (x)  für eine reelle Zahl  k > 0  in einer  U (x0) Df die Ungleichung
	(3)	| R (x) | k · ( x - x0 )²
	erfüllt.
Beachte schließlich   ( x - x0 )² = | x - x0 |²
Anmerkung:		L erinnert an Lipschitz, einen Mathematiker, der ähnliche Bedingungen wie (3) formuliert hat. Wie bereits angedeutet, gibt es einen allgemeineren Differenzierbarkeitsbegriff, der aber etwas schwieriger zu handhaben ist, ohne für die Schulmathematik Vorteile zu bringen. In diesem Skript wird die Differenzierbarkeit ausschließlich im Sinne der definierten L-Differenzierbarkeit verwendet und künftig wird in der Regel das L fortgelassen.

Es sei weiter erklärt

	Wenn  f  gemäß der letzten Definition L-differenzierbar ist, heißt die Zahl  m  die Ableitung von  f  an der Stelle  x0 .
	Bezeichnung	m = f ' (x0)     (lies: "f gestrichen von x0")
	Die lineare Funktion
		x f (x0) + f ' (x0) · ( x - x0 )
	heißt Tangente an der Kurve von  f  im Punkt ( x0 | f (x0) ) .

Um die Diffenrenzierbarkeitsdefinition zu rechtfertigen, muss noch gezeigt werden, dass  m  eindeutig bestimmt ist.

	Ist nämlich für k, + in U (x0) Df
	f (x) = f (x0) + m ( x - x0 ) + R (x)	mit | R (x) | k ( x - x0 )²
und	f (x) = f (x0) + ( x - x0 ) + (x)	mit | (x) | ( x - x0 )²
so folgt durch Subtraktion der Gleichungen und leichtes Umformen
	( m - ) ( x - x0 ) = (x) + ( - R (x) )
und daraus
	| m - | ( + k ) · | x - x0 |	( x x0 )
und daher nach Satz 16 (Archimedisches Axiom)
	m =

Abschließend sei bemerkt, dass das Interesse vornehmlich Funktionen gilt, die über einem Intervall definiert sind. Es kann einfach erklärt werden, eine Funktion sei über einem Intervall differenzierbar, wenn sie an jeder Stelle des Intervalls differenzierbar ist. Dann kann es in der Differenzierbarkeitsbedingung allerdings zu jedem  x  ein anderes  k  geben. Bequemer ist daher folgende etwas stärkere Definition:

	Die Funktion  f  heißt über dem Intervall [ a | b ]   L-differenzierbar mit der Ableitungsfunktion  f ' , wenn es eine Konstante  k > 0  gibt, so dass für alle x, x0  [ a | b ]
		| f (x) - f (x0) - f ' (x0)( x - x0 ) | k (x - x0 )²
	ist.
Anmerkung:	k  ist hier gemeinsame Konstante für alle x0  [ a | b ] . Man beachte die Definition der L-Differenzierbarkeit. R (x) = f (x) - f (x0) - f ' (x0)( x - x0 ) . Der Eindeutigkeitsbeweis (s. o.) ist Voraussetzung für die Existenz der Ableitungsfunktion f ' (x).

Aufgaben zu 5.2

weiter zu    5.3 Die Ableitung der ganzrationalen Funktionen  

 zurück zu MATHEMATIK Übersicht