|
Oberstufe: Differential- und Integralrechnung |
| Oberstufenskript Differential- und Integralrechnung für Grund- und Leistungskurse von Jürgen Rohde |
zurück zum INHALT |
11. Mittelwertsätze
12. Verkettung von Funktionen - Ableitungsregeln
Die sogenannten rationalen Verknüpfungen ( + , - , · , : ) von Funktionen sind bekannt. Funktionen sind definitionsgemäß Abbildungen. Zwei Abbildungen lassen sich miteinander verknüpfen, indem man sie nacheinander ausführt. Beispiele sind bekannt aus der Geometrie (Kongruenzabbildung, Ähnlichkeitsabbildung, u.a.) und lassen sich aus dem Fotobereich ausdenken (z.B. Kopien, Vergößerungen).
Aus dem Bereich der Funktionen betrachte man das folgende Beispiel:
h (x) = 
.
Die Funktionswerte von h kann man auf "natürliche" Weise in zwei Schritten berechnen:
| 1. x | g | 2 - x = z und 2. z | f |  |
 |
|
|||
Die Funktionen g und f sind sicher elementarer als h . Man kann h als Zusammensetzung von g und f in dieser Reihenfolge auffassen. Auch die Bezeichnung "Verkettung von g und f " ist anschaulich.
| Man schreibt: | h = f  g |
(gelesen f nach g ) | oder auch | h (x) = f ( g (x) ) . |
Wenn man eine Funktion als Maschine deutet, welche zu jeder Eingabe x eindeutig die Ausgabe f (x) liefert, und die Maschine als "black box" durch einRechteck darstellt, erhält man folgende instruktive Illustration der Verkettung
| x |  |
 |
|
g (x) = z | |
 |
|
f (z) = f ( g (x) ) = f g (x) = h (x) |
|
| x | |
|
|
 |
|
|
|
|
|
Wenn man die Funktionen in der umgekehrten Reihenfolge verkettet, erhält man
k (x) = 2 - 
,
d.h. die Verkettung
von Funktionen ist nicht kommutativ.
Man kann die Funktionen auch grafisch verketten und die Kurve der Verkettung zeichnen,
ohne einen einzigen Funktionswert zu berechnen.
Erklären Sie das folgende Darstellungsverfahren:
f .
(Man verwende kariertes Papier oder Millimeterpapier. Die gefärbten Linien können entfallen.)
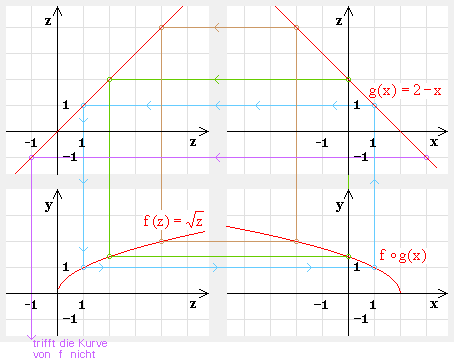
Beispiel:
|
Es sei g (x) = x² und f (x) = sin x .
Dann ist f g (x) = sin x² bzw.
g f (x) = ( sin x )² . Zeichne die Maschinenbilder und stelle beide grafisch dar. |
Es ist einleuchtend, dass man auch mehr als zwei Funktionen verketten kann, z.B.:
g (x) = x² , f (x) = sin x , e (x) = 1/x .
Dann ist e
f g (x) = 1/sin x² .
weiter zu
Ableitungsregeln
