 |
AUFGABEN zu Differential-/Integralrechnung
|
Aufgaben zu
12. Verkettung von Funktionen - Ableitungsregeln
- Verkette jeweils f mit g und g mit f :
| a. | f (x) = a x² + b x + c |
| g (x) = m x + b |
| b. | f (x) = x³ |
| g (x) = x - 3 |
| c. | f (x) = 1/x |
| g (x) = ( x - 2 )4 |
| d. | f (x) = 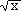 |
| g (x) = x³ + 2 x² + 3 x + 2 |
| e. | f (x) = 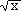 |
| g (x) = -( x + 3 )² - 2 |
- Schreibe folgende Funktionen als Verkettung einfacher!
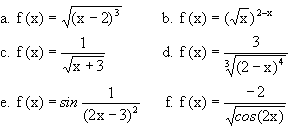
- Welche Voraussetzungen müssen erfüllt sein, damit man zwei (drei) Funktionen miteinander verketten kann?
-
Zeige, dass immer e
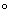 ( f
( f 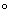 g ) =
( e
g ) =
( e 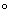 f )
f ) 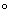 g ist.
Welches Gesetz ist es?
g ist.
Welches Gesetz ist es?
- Erweitere das Darstellungsverfahren zur graphischen Verkettung
auf 3 Funktionen.
- Formuliere einen Satz über die Ableitung der Verkettung von drei Funktionen
und verallgemeinere auf n Funktionen.
- Entwickle eine Regel zur Ableitung eines Produktes von 3 Funktionen und verallgemeinere.
- u, w, v seien differenzierbare Funktionen und
w (x)
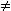 0
und v (x)
0
und v (x) 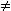 0 .
0 .
| Bilde ( |
u · v |
) ' und ( |
u |
) ' |
 |
 |
| w |
v · w |
- Zeigen Sie
|
u.a. mit Hilfe der Beispiele aus 12. : |
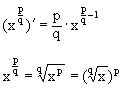 |
| Potenzregel für rationale Exponenten |
| Beachte: |
- Zeige, dass L-Stetigkeit mit Verkettung von Funktionen verträglich ist.
Deute zur Unterstützung die folgende Ungleichnungskette:
| f ( g (x) ) - f ( g (x0) ) |
 Lf · | g (x) - g (x0) |
Lf · | g (x) - g (x0) |
 Lf · Lg · | x - x0 | .
Lf · Lg · | x - x0 | . |
- Leiten Sie - wenn möglich - zweimal ab und geben Sie den Bereich an, über dem die Ableitungen existieren.
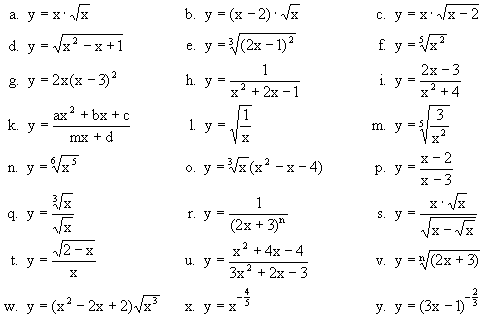
- Bestimme ( f
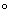 f ) ' und
( f
f ) ' und
( f 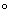 f
f 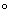 f ) '
unter der Voraussetzung der Ableitbarkeit.
f ) '
unter der Voraussetzung der Ableitbarkeit.
- Bestimmen Sie für f (x) = x² die Funktionen
( f
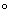 f ) ' ;
f '
f ) ' ;
f ' 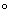 f ;
f
f ;
f  f ' ;
f '
f ' ;
f '  f ' .
f ' .
- Bestimme unter der Voraussetzung der Differenzierbarkeit die Ableitung von
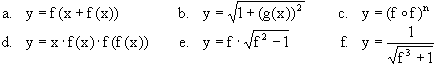
- u, v seien mindestens 4-mal differenzierbar. Berechne
a. ( u · v ) ''
b. ( u · v ) '''
c. ( u · v ) (4) d.i. 4. Ableitung
- Zeige: f (x) = x³ + 3 x
ist umkehrbar über
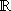 .
Kann man die Gleichung der Umkehrfunktion explizit angeben? Berechne
.
Kann man die Gleichung der Umkehrfunktion explizit angeben? Berechne
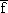 ' (4) ;
' (4) ;
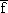 ' (0) ;
' (0) ;
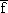 ' (-4) ;
' (-4) ;
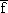 ' (36) ;
' (36) ;
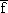 ' (-14) .
' (-14) .
- Berechne
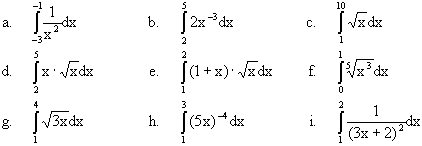
- Untersuche die Funktionen
| fa (x) = |
ax |
für a > 0 . |
 |
| a x² + 1 |
Wie ändern sich die y-Werte für wachsende | x | ?
Zeichne die Kurve für a = 1 und a = 2,25 .
Auf welcher Kurve liegen die Extrempunkte, auf welcher die Wendepunkte?
- Ein symmetrisch zur y-Achse gelegenes Rechteck hat zwei Eckpunkte auf der x-Achse,
die beiden anderen liegen auf der Kurve y = 4 / (x² + 1 ) .
Welches dieser Rechecke hat extremen Inhalt?
- In einem Kegel soll ein Zylinder mit maximaler Oberfläche einbeschrieben werden.
weitere Aufgaben zu
13. Winkelfunktionen
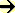
 zurück zu MATHEMATIK Übersicht
zurück zu MATHEMATIK Übersicht
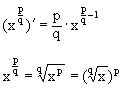
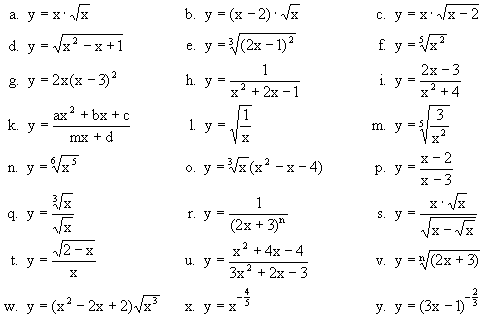
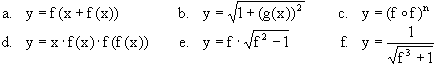
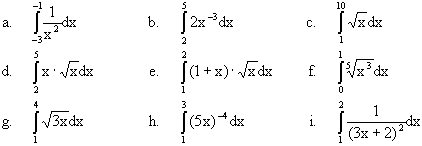
![]()