netSCHOOL AUFGABEN zu Differential-/Integralrechnung
[  I N H A L T  ]     [ MATHEMATIK Übersicht ]

Aufgaben zu
13. Winkelfunktionen
13.1 Bogenmaß

  1. Fülle die Leerstellen in der folgenden Tabelle aus
    in Grad 10°     23° 514°   1265°     2° 218°
    arc   1 0,1     2,56   0,724 75    

    Beachte:   arc = /180° ·     und     = 180°/ · arc
13.2 Polarkoordinaten

  1. Zeichne
    a.  P ( 2 ; 90° )     b.  P ( 3 ; 180° )     c.  P ( 2,5 ; -90° )     d.  P ( 1 ; 520° )
    e.  P ( 4 ; -1000° )     f.  P ( 3 ; 2 )     g.  P ( 3 ; 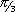)     h.  P ( 2 ; -2 /5 )
13.4 Eigenschaften der trigonometrischen Funktionen

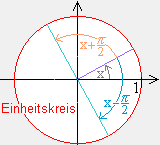
  1. Bergründen Sie am Einheitskreis folgende Beziehungen
    1. sin (-x) = - sin x         (die Funktion sin ist ungerade)
    2. cos (-x) = cos x           (die Funktion cos ist gerade)
    3. sin ( x + ½ ) = cos x
    4. cos ( x - ½ ) = sin x
    5. sin ( ½ - x ) = cos x
    6. cos ( ½ - x ) = sin x
    7. sin² x + cos² x = 1
    8. sin ( x + 2 ) = sin x
    9. cos ( x + 2 ) = cos x
      Die Funktionen sin und cos haben die Periode  2
    10. Welche Periode haben die Funktionen tan und cot ?

  1. Schreibe alle Nullstellen auf
    a.  sin x     b.  cos x     c.  tan x
    d.  sin 2 x     e.  sin ½ x     f.  sin ( x + )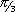
    g.  sin ( 2 x + 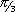)     h.  sin ( x/3 - 2 )     i.  cos ( 3 x + ½ )

  2. Welche Periode haben die Funktionen
    a.  y = sin 2 x     b.  y = cos x/2     c.  y = cos ( - 2 x )     d.  y = tan x/3
13.5 Streckung von sin-Kurven in x- und y-Richtung

  1. Zeichne je eine Periode der Kurve
    a.  y = - 2 sin x     b.  y = 3 cos x             c.  y = 2 cos ( x - /6 )
    d.  y = 4 sin ( 3 x + )     e.  y = ¼ cos ( x/2 - /2 )

  2. Zeichne durch Überlagerung (Addition) zweier Kurven
    a.  y = sin x + cos x     b.  y = sin x + 2 sin 2 x
    c.  y = x + sin x     d.  y = x² + sin x
    e.  y = 2 sin x + 3 cos x     f.  y = cos x/2 + sin 2 x

  3. Im Dreieck ABC seien   ,    und  a  gegeben. Berechne  b  und beweise so den Sinussatz.
        sin   =   a
    sin b

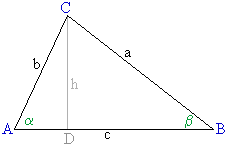
  4. Im Dreieck ABC seien  b ,  c  und    bekannt. Bestimme  a  und beweise so den Cosinussatz.

        a² = b² + c² - 2 b c · cos


13.6 Additionstheoreme

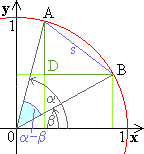
  1. Berechne die Sehne  s  auf zwei Arten:
    a.   Nach dem Cosinussatz aus   0AB
    b. Nach dem Satz des Pythagoras aus   ADB.
      Zeige:   | B D | = cos - cos
        | A D | = sin - sin
    c.   Durch Gleichsetzung der beiden Werte für s² erhält man das Additionstheorem.
       ( A )   cos ( - ) = cos · cos + sin · sin

  2. Ersetzt man    durch ( - ) , erhält man aus ( A ) in Aufgabe 10.:
                   cos ( + ) = cos · cos - sin · sin

  3. Leite aus Aufgaben 10. und 11. die Additionstheoreme
          sin ( + ) = sin · cos + cos · sin     und
    sin ( - ) = sin · cos - cos · sin     her.
    Setze dazu in ( A ) für     ( 90° - ) und danach   ( - ) für    .

  4. Leite aus den Additionstheoremen her:
    a.   sin 2  =  2 cos sin         b.   cos 2  =  cos² - sin²
    c.   tan ( ± )     d.   tan 2  =  2 tan      
    1 - tan²
    e.   sin²  =  ½ ( 1 - cos 2 )     f.   cos  =  2 cos² /2  -  1

  5. Zeige:
          sin x + sin y  =  2 · sin  x + y  · cos  x - y
    2 2
      sin x - sin y  =  2 · sin  x - y  · cos  x + y
    2 2
    (Hinweis: Setze  x = +   und  y = -   und wende geeignete Additionstheoreme an.)
 

weitere Aufgaben zu    13.7 Lineare Approximation der sin-Funktion  

 zurück zu MATHEMATIK Übersicht