Oberstufe: Differential- und Integralrechnung

Oberstufenskript Differential- und Integralrechnung für Grund- und Leistungskurse von Jürgen Rohde

zurück zum INHALT

 12. Verkettung von Funktionen - Ableitungsregeln

 
13. Winkelfunktionen

13.1 Bogenmaß

Für das Folgende ist es nützlich, die Winkelmessung an das metrische System anzuschließen. Dazu erinnere man sich daran, dass

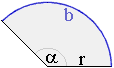
b =	r	·
	180°

der Bogen eines Kreisausschnittes mit dem Mittelpunktswinkel    ist. Also ist

	Bogen	=	b	=		·       nur vom Winkel abhängig
	Radius		r		180°

und kann daher als Maß des Winkels dienen. Dieses Maß wird als Bogenmaß von oder arc (arcus) bezeichnet und hat die Einheit  rad  (Radiant).

Es ist also     arc 1°  =		· 1° rad 0,01745 rad  .
	180°

In der folgenden Tabelle finden Sie die wichtigsten Winkel in Grad- und Bogenmaß.

in Grad	180°	90°	45°	30°	60°	1°	360°	720°
arc		/2	/4	/6	/3	/180	2	4

 

13.2 Polarkoordinaten

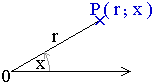Die Lage eines Punktes in der Ebene wurde bisher nach Auszeichnung zweier sich schneidenden Geraden als Koordinaten-Achsen durch ein Zahlenpaar  ( x | y )  - den kartesichen Koordinaten - beschrieben. Man kann die Lage eines Punktes aber auch eindeutig beschreiben, indem man einen Punkt  0  und eine von ihm ausgehende Halbgerade auszeichnet. P ( r ; x )  ist dann der Punkt der Ebene, der von  0  den Abstand  r  und dessen Fahrstrahl  OP  mit der festen Halbgeraden den Winkel  x  bildet. Das Winkelmaß  x  kann dabei jede reelle Zahl annehmen.

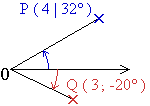Es ist dann
P ( 4 | 32° ) = P ( 4 ; 32° ± 360° · k )
oder allgemein
P ( r ; x ) = P ( r ; x + 2 k )       k ;  x  im Bogenmaß
( r ; x ) heißen Polarkoordinaten von  P .
 

13.3 Definition der trigonometrischen Funktionen

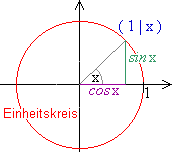Die kartesischen Koordinaten des Punktes  ( 1 ; x )  in Polarkoordinaten
heißen ( cos x | sin x ) .

	tan x  =	sin x		;       x	2 k + 1	·
		cos x			2
	cot x  =	cos x		;       x	k  ·
		sin x

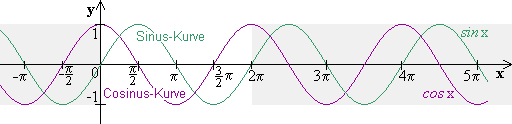
13.4 Eigenschaften der trigonometrischen Funktionen

In den Aufgaben 3 bis 5 begründen Sie selbst verschiedene Beziehungen der trignometrischen Funktionen und finden ungerade/gerade Funktionen, Periodizität, Nullstellen.

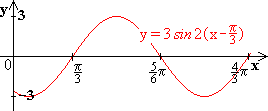
13.5 Streckung von sin-Kurven in x- und y-Richtung

Anstelle die Kurven zu transformieren, kann man auch das Koordinatensystem transformieren. Hier folgen 4 Beispiele:

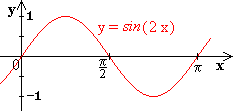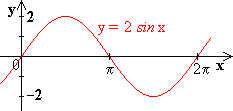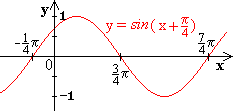In den Aufgaben 8 und 9 beweisen Sie den Sinussatz und den Cosinussatz (Wiederholung).

	Sinussatz	Im Dreieck ABC seien  , und  a  gegeben.
		Dann gilt:	sin   =   a sin b

	Cosinus- satz	Im Dreieck ABC seien  b ,  c  und    bekannt.
		Dann gilt:	a² = b² + c² - 2 b c · cos

 

13.6 Additionstheoreme

In den Aufgaben 10, 11 und 12 erarbeiten Sie die Additionstheoreme.

	Additions- theoreme	sin ( + ) = sin · cos + cos · sin
		sin ( - ) = sin · cos - cos · sin
		cos ( + ) = cos · cos - sin · sin
		cos ( - ) = cos · cos + sin · sin

weiter zu    13.7 Lineare Approximation der sin-Funktion  

 zurück zu MATHEMATIK Übersicht