Oberstufe: Differential- und Integralrechnung

Oberstufenskript Differential- und Integralrechnung für Grund- und Leistungskurse von Jürgen Rohde

zurück zum INHALT

 13. Winkelfunktionen

 
13.7 Lineare Approximation der sin-Funktion

Vorübung: Vergleiche die Werte von  cos x  und  1  bzw.  sin x  und  x  für  | x | < 0,1  .

Wegen

( 1 )	sin ( x + h )  =  sin x · cos h  +  cos x · sin h
	und  sin h h   und  cos h 1      für kleine | h |

kan man

( 2 )

lx (h) = sin x + h · cos x

als lineare Approximation der sin-Funktion bei  x  mit der Ableitung

sin ' x = cos x

vermuten.
Beweis: Wenn man von ( 1 ) den rechten Term von ( 2 ) subtrahiert, folgt

| R (h) |	= | sin ( x + h ) - lx (h) | = | sin x ( cos h - 1 ) + cos x ( sin h - h ) |
	| sin x | · | cos h - 1 | + | cos x | · | sin h - h |                 [ | sin x | 1  ;   | cos x | 1 ]
( 3 )	| cos h - 1 | + | sin h - h |  .

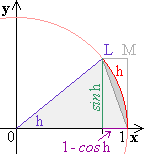
Aus der Figur links liest man ab, da "Sehne < Bogen" :

( sin h )² + ( 1 - cos h )²    h² ,   d.h.
( 4 )	1 - cos h    ½ h²

Weiter hat das Dreieck 01L den Inhalt ½ sin h , der Sektor 01L den Inhalt ½ h und der Kreisabschnitt 1L1 (dunkler grau) ist der Fläche nach kleiner als das Dreieck LM1 . Daraus folgt für  | h | < ½

( 5 )	| sin h - h |		| sin h |  · | 1 - cos h |		| 1 - cos h |	½ h²
	2x Inhalt des Kreisabschnitts		2x Inhalt des Dreiecks LM1	beachte auch | sin h | 1

Wegen ( 4 ) und ( 5 ) folgt aus ( 3 )

| sin ( x + h ) - lx (h) |  =  | R (h) |   ½ h² + ½ h²   1 · h²  .

 

13.8 Die Ableitung weiterer Winkelfunktionen und ihrer Umkehrung

Wegen	cos x = sin ( x + ½ )
folgt nach der Kettenregel
	cos ' x  =	cos ( x + ½ ) =	- sin x	(Kontrolle: Einheitskreis)
Mit Hilfe der Quotientenregel erhalten Sie über dem Definitionsbereich
	tan ' x  =   1           und            cot ' x  =  -  1 cos² x sin² x

Die Winkelfunktionen sind nur abschnittsweise umkehrbar und haben beliebig viele Umkehrfunktionen, von denen man nach Vereinbarung eine auswählt. Sie sind in folgender Tabelle zusammengestellt.

Funktion f	Definitions- breich f	Umkehrfkt.	Definitions- breich	'
sin	[ - ½ | ½ ]	arcsin	[ - 1 | 1 ]	x		;   | x | 1
cos	[ 0 | ]	arccos	[ - 1 | 1 ]	x -		;   | x | 1
tan	] - ½ | ½ [	arctan	] - | + [	x	1
					1 + x²
cot	] 0 | [	arccot		x -	1
					1 + x²

Beweise der Ableitungsregeln:

1. sin x = y    x = arcsin y       für  x [ - ½ | ½ ] ,  y [ - 1 | 1 ]
      
   cos x =   ( cos x  ist in  [ - ½ | ½ ]  nicht negativ).
   

   Also	arcsin ' y  =	1	=	1	=	1	oder wenn die Variable  x  heißt:
   		sin ' x		cos x
   	arcsin ' x  =			;	x ] - 1 | + 1 [

   
   
2. Analog folgt die Ableitung von arccos
   y = cos x    x = arccos y        x [ 0 | ] 
      
   sin x =
   

   Also gilt	arccos ' y  =	1	=   -	1	in  ] -1 | + 1 [
   		- sin x

   
   
3. y = tan x    x = arctan y
   

   arctan ' y  =	1	=	1	=  cos² x  =	1	,     denn cos² x  =	1
   	tan ' x		1		1 + y²		1 + tan²
   			cos² x

   
   (Zur Begründung dividiere sin² x + cos² x = 1   durch   cos² x .)

4. Beweise als Aufgabe 16 :

   	arccot ' y  =  -	1
   		1 + y²

weiter zu    13.9 Stammfunktionen der Winkelfunktionen  

 zurück zu MATHEMATIK Übersicht