AUFGABEN zu Differential-/Integralrechnung

Aufgaben zu
9. Einführung in die Integralrechnung

Aufgaben zur Wiederholung und Vertiefung

1. Begründe die Formel  F = a · b  für den Inhalt eines Rechtecks mit den Seiten  a  und  b , falls
   1.  a  und  b  kommensurabel (d.h. ein gemeinsames Maß haben -
      vgl. auch den Begriff des gemeinsamen Teilers),
   2.  a  und  b  nicht kommensurabel sind.

2. Leite Inhaltsformeln für Dreieck, Parallelogramm, Trapez her

   

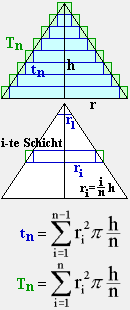
3. Kegelinhalt durch Schichtenmethode
   Die Abbildung rechts zeigt den Achsenschnitt durch einen Kegel mit ein- und umbeschriebenem Treppenkörper, bestehend aus gleichhohen zylindrischen Scheiben.
   Zeige, dass die Inhalte der einbeschriebenen (  t_n ) und der umbeschriebenen (  T_n  ) Treppenkörper für beliebig große  n  den gemeinsamen Grenzwert  V = 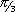  r² h  haben. (vgl. 3., Aufgabe 3)

4. Bestimme mit der Schichtenmethode das Volumen
   1. einer Pyramide,
   2. einer Halbkugel.

1. Zeichne die Inhaltsfunktion zur gegebenen Randfunktion  f  über dem Intervall  [ a | b ]  und gib auch die Gleichnung der Inhaltsfunktion analog zu der von  f  an.
   

   a.	f (x) =	{	-2   in  [ -3 | -1 ]    3   in  ] -1 |  2 ]    0   in  ]  2 |  4 ]  -1   in  ]  4  |  6 ]		b.	f (x) =	{	-1/2   in    [ -2 | 0 ]   4/3   in    ]  0 | 3 ]  -1/3   in    ]  3 | 6 ]
   c.	f (x) =	- ½ x + 3   über  [ -4 | 4 ]			d.	f (x) =	- 2 x + 4   über  [ -4 | 2 ]
   e.	Führe Beispiel 3 im einzelnen aus.
   f.	Führe Beispiel 3 auch für den Fall durch, dass die Gerade die x-Achse schneidet; desgleichen für den Fall, dass das Geradenstück über  [ a | b ]  unter der x-Achse liegt.

2. Führe Beispiel 5 im einzelnen aus.
3. Bestimme die Inhaltfunktion nach den Methoden der Beispiele 4 und 5 auch für folgende Funktionen:
   1.  f (x) = x²  ,   [  3 | 8 ]
   2.  f (x) = x²  ,   [ -3 | 8 ]
   3.  f (x) = 2 x²  ,   [ 0 | 4 ]
   4.  f (x) = ½ x²  ,   [ 0 | 5 ]
   5.  f (x) = a x²  ,   [ 0 | b ]
   6.  f (x) = x² + x  ,   [ 0 | b ]
   7.  f (x) = x³ - x²  ,   [ 0 | b ]
   8.  f (x) = -2 x³ + x² - 4 x + 1  ,   [ 0 | b ]
4. Die Folge  a₁, a₂, a₃, . . . , a_n, . . .   sei monoton und beschränkt, d.h.  a_n+1 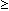 a_n  für alle  n  und  | a_n |  S  für alle  n  und eine positive Zahl  S .
   

   Zeige:	Dann gibt es genau eine Zahl  W  mit folgender Eigenschaft: In jeder Umgebung (offene Intervalle!) um  W  liegen, mit Ausnahme endlich vieler, alle Glieder der Folge  an .
   Anm. :	W  heißt Grenzwert der Folge  an .

5. Zeige durch Intervallschachtelung: Es gibt eine positive reelle Zahl, deren Quadrat  3  ist.

weitere Aufgaben zu    9.2 Hauptsatz der Differential- und Integralrechnung  

 zurück zu MATHEMATIK Übersicht