netSCHOOL Oberstufe: Differential- und Integralrechnung

Oberstufenskript
 Differential- und Integralrechnung
 für Grund- und Leistungskurse von Jürgen Rohde		    zurück zum INHALT
 9.1 Inhaltsfunktion

 
4. Beispiel

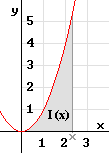
Parabel
Nun wird das erste nicht-lineare Beispiel betrachtet, die quadratischen Funktion mit der Gleichung
 f (x) = x²
über dem Intervall  [ 0 | b ] .

Die Inhaltsfunktion lässt sich nun nicht mehr durch elementare Flächenberechnung bestimmen. Es liegt aber nahe, die Inhaltsfunktion durch "elementare Flächen" zu approximieren. Das gelingt z.B., wenn man die Parabel, also die Randfunktion, durch untere und obere Treppenfunktionen einschließt (siehe Bild rechts).
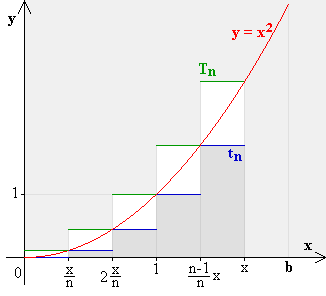
Parabel
 x  sei eine Zahl aus  [ 0 | b ] . Wir teilen das Interval  [ 0 | x ]  in  n  gleichlange Teilintervalle, jedes von der Länge  x/n .
Zu dieser Zerlegung des Intervalles  [ 0 | x ]  ist im nebenstehenden Bild eine untere Treppenfunktion  tn  und eine obere Treppenfunktion  Tn  eingezeichnet.
Dann gilt offensichtlich:
tn  <  I (x)  <  Tn   .
 
Über jedem Teilintervall kann man die weißen Flächen alle nach rechts auf den letzten Streifen zusammenschieben; er wird dann genau ausgefüllt. Man liest ab:
(1)     Tn  - tn    =    x 
  n		 · x² =  x³
n
 
Das bedeutet, dass die Differenz der Integrale der oberen und unteren Treppenfunktion beliebig klein wird, wenn nur  n  beliebig groß wird.
 
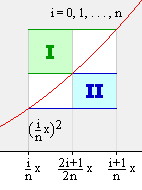Parabel Zur Verbesserung der Genauigkeit wird man die Zerlegung "verfeinern", z.B. jedes Teilintervall halbieren, d.h. die Zahl der Teilintervalle verdoppeln. Dann nimmt das Integral der oberen Treppenfunktion über jedem Teilintervall um die farbige Fläche  I  ab und das Integral der unteren Treppenfunktion um die farbige Fläche  II  zu (siehe Ausschnitt im Bild links).
Also ist die Ungleichungskette
(2)     tn  <  t2n  <   I (x)  <  T2n  <  Tn 

und zudem die Gelichung
(3)     T2n  -  t2n  =  ½ (  Tn  -  tn ) 

bestätigt. (Bemerkung: Die Integrationsgrenzen können fortgelassen werden, wenn Klarheit besteht.)
Aus diesen Überlegungen - zusammengefasst in den Aussagen  (1)  bis  (3)  - folgt, dass
    [  tn  |  Tn  ] 
eine Intervallschachtelung (siehe: Axiom der Intervallschachtelung) bestimmen, bei der die Länge der Intervalle beliebig klein wird. Es gibt nach dem Axiom der Intervallschachtelung genau eine Zahl, welche in allen Intervallen enthalten ist. Diese Zahl wird hier als  I (x)  definiert. Nachdem man nun weiß, dass es eine solche Zahl  I (x)  gibt, soll sie "berechnet" werden.

Es ist nach Bild oben ( y = x² ):
    Tn = x
n		 [ 1² · ( x
n		 )² + 2² · ( x
n		 )² + 3² · ( x
n		 )² + . . . + n² · ( x
n		 )² ]
= x³
n³		 ( 1² + 2² + 3² + . . . + n² )
= x³
n³		 · n · ( n + 1 ) · ( 2 n + 1 )
               6		 (vgl. 3., Aufgabe 3)

Wenn  n  beliebig groß wird, unterscheidet sich  ( n + 1 )  beliebig wenig von  n  und entsprechend  ( n + 1 )  von  2 n .
Tn   unterscheidet sich für große  n  also beliebig wenig von  1
3		  x³ .
Es wird daher definiert
        I (x) =  1
3		  x³     als Inhaltsfunktion zur Randfunktion  f (x) = x²  .

 
5. Beispiel     (vergleiche Aufgabe 2)

Für die Randfunktion  f (x) = x³  findet man nach ganz analogen Überlegungen unter Beachtung von 3., Aufgabe 4
        I (x) =  1
4		  x4     für  x  [ 0 | b ] .

Ergänzungen zu den Beispielen 4 und 5
Hier geht es um den Existenznachweis einer bestimmten reellen Zahl. Dazu wurde wesentlich das Intervallschachtelungsaxiom benutzt. Es sei hier noch einmal unabhängig von den Beispielen formuliert:
 
Axiom der Intervallschachtelung
  Es sei  In = [ an | bn ]  eine Folge ineinander liegender Intervalle.
Die Länge  bn - an  der Intervalle werde beliebig klein.
Dann gibt es (genau*) eine reelle Zahl  c , welche in allen Intervallen liegt.
*) "genau" braucht nicht gefordert zu werden, weil man leicht zeigen kann (wie?),
dass es höchstens eine solche Zahl gibt.

Anmerkung:

  1. Wir sagen auch: Die Intervallschachtelung  [ an | bn ]  bestimmt die Zahl  c .
  2. In den Beispielen ist  bn - an = const / 2n  und wird daher beliebig klein werden, wenn  n  nur hinreichend groß ist. In diesem Fall sagt man etwas schärfer:
    Die Folge  bn - an  konvergiere geometrisch gegen Null.

Aus der Sekundarstufe I sollte eigentlich die Idee der Intervallschachtelung bekannt sein, z.B. bei der Einführung der nicht rationalen Zahl   .

Es kann übrigens die Zahlenmenge    nun axiomatisch beschrieben werden.
Die Menge    mit den Operationen  +  und  ·  erfüllt

  1. die Körperaxiome,
  2. die Anordnungsaxiome,
  3. das Archimedische Axiom und
  4. das Intervallschachtelungsaxiom.
Jede Menge mit zwei Verknüpfungen, die diese Axiome erfüllt, heißt vollständig angeordneter Körper.
   ist in folgendem Sinne vollständig:
Jede Obermenge von   , in der alle Axiome 1. - 4. gelten, ist    selbst. Oder anders ausgedrückt: Es gibt keine echte Obermenge von   , in der alle Eigenschaften von    gelten.

Die Axiome 3. und 4. werden künftig zum sogenannten Vollständigkeitsaxiom zusammengefasst.

Aufgaben zu 9.1

weiter zu    9.2 Der Hauptsatz der Differential- und Integralrechnung  

 zurück zu MATHEMATIK Übersicht