Oberstufe: Differential- und Integralrechnung

Oberstufenskript Differential- und Integralrechnung für Grund- und Leistungskurse von Jürgen Rohde

zurück zum INHALT

 8.3 Extremwertaufgaben

 
9. Einführung in die Intergralrechnung

 
In der Sekundarstufe I wurde die Inhaltsberechnung von Rechtecken, Dreiecken, Vielecken, Kreisen, Würfeln, Quadern, Prismen, Pyramiden, Kegeln, Kugeln u.a. erarbeitet. Aufgabe der Integralrechnung ist die Verallgemeinerung des Inhaltsproblems auf z.B. krummlinig begrenzte Flächen und weniger spezielle räumliche Figuren. Dabei werden Lösungswege erarbeitet, die auf viele außergeometrische Probleme anwendbar sind.

Aufgaben zur Wiederholung und Vertiefung

 
9.1 Inhaltsfunktion

Es wird mit sehr einfachen Funktionen begonnen, nämlich solchen, die stückweise konstant sind, den sogenannten Treppenfunktionen.

1. Beispiel
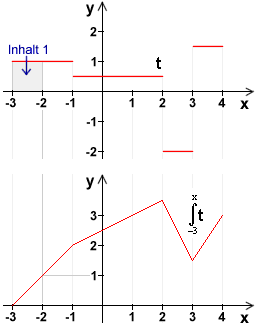   Im Bild ist die Funktion  t  dargestellt, mit

   t (x) =	{	1 , wenn  x  [ -3 | -1 ]
   		1/2 , wenn  x  ] -1 |  2 ]
   		-2 , wenn  x  ]  2 |  3 ]
   		3/2 , wenn  x  ]  3 |  4 ]

   Zur Funktion  t wird eine neue Funktion konstruiert über den Definitionsbereich  [ -3 | 4 ] .

   Diese neue Funktion wird bezeichnet mit  (lies: Integral von  t  von  -3  bis  x )

   Dieses Integral ist gleich der Summe der Rechteckinhalte, welche zwischen dem Graphen von  t  und der x-Achse über dem Intervall  [ -3 | x ]  liegen. Dabei zählen Inhalte von Rechtecken oberhalb der x-Achse positiv, unterhalb der x-Achse negativ.
   Daraus ergibt sich für  t  folgende Wertetabelle:
   

   x	-3	-2	-1	0	1	2	2,5	3	4
   	0	1	2	2,5	3	3,5	2,5	1,5	3

   
   Zwischen der Funktion  t  und der neuen Integral-Funktion gibt es natürlich enge Zusammenhänge. Aus der Kenntnis der einen kann man auf die andere schließen; graphisch gesehen von oben nach unten (siehe Abbildungen oben) und von unten nach oben. Der Funktionswert dieser Integral-Funktion ist die Summe der Rechteckinhalte von  t  über dem Intervall  [ -3 | x ]  unter Berücksichtigung des Vorzeichens. Umgekehrt gilt für alle  x  [ -3 | 4 ]  mit Ausnahme der Sprungstellen: Die Steigung dieser Integral-Funktion ist an der Stelle  x  gleich dem Funktionswert von  t  bei  x .

   Beachte:   An den Sprungstellen von  t  hat die Integral-Funktion einen Knick, also keine Steigung.

Funktionen wie  x

werden küftig auch als Inhaltsfunktionen bezeichnet.

2. Beispiel
   

   Es sei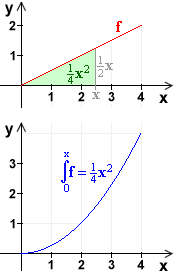
   	f (x)	= ½ x	über [ 0 | 4 ]
   Dann ist
   I (x) =		= ¼ x²	über [ 0 | 4 ]

3. Beispiel (vergleiche Aufgabe 1 e)
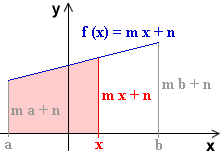   Im Bild ist die Randfunktion  f  mit  f (x) = m x + n  dargestellt. Die zugehörige Inhaltsfunktion
   

   I (x) =

   ordnet jedem  x [ a | b ]  den Inhalt eines Trapezes zu:
     I (x) = ½ ( m a + n + m x + n ) · ( x - a )   =  ½ m x² + n x - ( ½ m a² + n a )

weiter zu    4. Beispiel zur Inhaltsfunktion  

 zurück zu MATHEMATIK Übersicht