Oberstufe: Differential- und Integralrechnung

Oberstufenskript Differential- und Integralrechnung für Grund- und Leistungskurse von Jürgen Rohde

zurück zum INHALT

 8.2 Bestimmung von Funktionsgleichungen aus gegebenen Eigenschaften

8.3 Extremwertaufgaben

Beispiele:

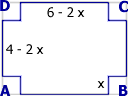14. Im Rechteck  A B C D  mit den Seiten  AB = 6 cm  und  BC = 4 cm  wird von den Ecken aus je ein Quadrat der Seitenlänge  x  abgeschnitten und die restliche Fläche zu einer offenen Schachtel gefaltet. Wie groß muß die Seite gewählt werden, damit der Inhalt der Schachtel möglichst groß wird?

    Lösung:
    Für der Inhalt der Schachtel gilt

    V = Grundfläche · Höhe
    V = ( 6 - 2 x ) · ( 4 - 2 x ) · x       V heißt Zielfunktion

    Laut Aufgabenstellung ist ein Maximum von  V  gesucht. Der Definitionsbereich von  V  ist durch die Problemstellung eingeschränkt auf  ] 0 | 2 [ .
    Aus
    V ( x ) = 24 x - 20 x² + 4 x³
    folgt
    V ' ( x ) = 24 - 40 x + 12 x²
    und
    V '' ( x ) = -40 + 24 x   .

    V ' ( x ) = 24 - 40 x + 12 x² = 0     x² - 10/3 x + 2 = 0
      x = 1/3 ( 5 + ) oder x = 1/3 ( 5 - )

    Davon liegt nur  x = 1/3 ( 5 - ) 0,785  im Definitionsbereich.
    Außerdem ist  V '' (0,785) < 0 .
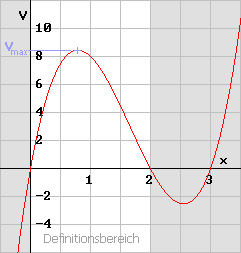
    Also ist  V (0,785) = 8,45  ein relatives Maximum.

    Eine Graphische Darstellung verdeutlicht den Verlauf der Zielfunktion.

     

15. 
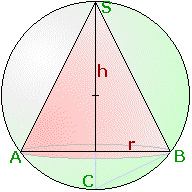    Wie hoch ist der einer Kugel mit dem Radius  R  einbeschriebene Kegel mit maximalem Volumen?
    Lösung:

    1. Schritt:
    Zeichnung, Achsenschnitt.  h, r  Höhe bzw. Radius des Kegels.
    Man beachte Strecke CS = 2 R (Kugeldurchmesser)

    2. Schritt:
    Aufstellen der Zielfunktion (Kegelvolumen):
    (1)   V = r² · h

    3. Schritt:
    Aufsuchen einer Randbedingung. Nach dem Höhensatz des Euklid gilt im Dreieck  B C S 
    (2)   r² = h · ( 2 R - h )

    4. Schritt:
    Elimination von Variablen in (1) , so dass die Zielfunktion nur noch eine Funktion einer Variablen ist. Hier folgt
    (3)   V (h) = h · ( 2 R - h ) · h · = ( 2 R h² - h³ )         h ] 0 | 2 R [

    5. Schritt:
    Formale Bestimmung eines relative Maximums. Weil der Faktor    die Lage der Extrema nicht verändert, genügt es, die Funktion  f  mit der Gleichnung

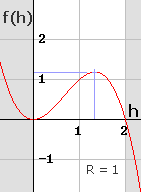    (3')   f (h) = 2 R h² - h³     zu untersuchen.

            f ' (h) = 2 R · 2 h - 3 h²

            f '' (h) = 4 R - 6 h

            f ' (h) = 0     h = 0   oder   h = R

    [ f ' ( R) = 0   und   f '' ( R) = - 4 R < 0 ]     f ( R) ist relatives Minimum.

    V ( R) = · ( 2 R · 16/9 R² - 64/27 R³ ) = 32/27 · · R³   (maximales Volumen)

    Anmerkung: Man beachte dass  R  eine Konstante ist.

Bei einer Reihe von Aufgaben treten Quadratwurzelterme auf. Solche Aufgaben lassen sich leicht lösen, wenn man das Quadrat der Zielfunktion auf relative Extrema untersucht. Denn es gilt
 

	Satz 10	Es sei  f (x0)  > 0 . Dann ist  f (x0)  genau dann relatives Maximum (Minimum) von  f , wenn  [ f (x0) ] ²  relatives Maximum (Minimum) von  f ²  ist.

Denn für positive  f (x) ,  f (x₀)  gilt in einer  U (x₀) 

	f (x)	<	f (x0)		[ f (x) ] ²	<	[ f (x0) ] ²	und
	f (x)	>	f (x0)		[ f (x) ] ²	>	[ f (x0) ] ²	.

Beispiel:

16. Wie hoch ist der einer Kugel vom Radius  R  einbeschriebener Kegel mit maximaler Mantelfläche? (Vergleiche Zeichnung zu Beispiel 15). Der Lösungsgang wird abgekürzt, soweit er wie in Beispiel 15 verläuft.
    Mantelfläche des Kegels:

    (1)   M = r s         (s = Seitenlinie des Kegels = Strecke BS)

    (2)   s ² = 2 R · h        nach Satz des Euklid im Dreieck BCS

    (3)   r ² = h · ( 2 R - h )       (s. Beispiel 15 (2) )

    Wegen der beiden Randbedingungen (2) und (3) wird (1) quadriert:

    (4)   M ² = ² r ² s ² = ² h · ( 2 R - h ) · 2 R · h = 2 R · ² · [ h ² ( 2 R - h ) ]

    und untersuchen die Funktion

    (5)   f (h) = h ² ( 2 R - h ) = 2 R h ² - h ³

            f ' (h) = 4 R h - 3 h ²

            f '' (h) = 4 R - 6 h  ,

    dies sind übrigens dieselben Gleichnungen wie in Beispiel 15, also ergibt sich auch dieselbe Lösung  h =  R  .

weiter zu    9. Einführung in die Intergralrechnung  

 zurück zu MATHEMATIK Übersicht