AUFGABEN zu Differential-/Integralrechnung

Aufgaben zu
8. Anwendungen II

8.3 Extremwertaufgaben

1. Zerlege die Zahl  20  so in zwei Summanden, dass das Produkt des einen mit dem Quadrat des zweiten am größten wird.
2. Bestimme das Maximum von  f (x) = 4 x³ - 8 x² + 5 x  für  0 x 1 . Beachte die Randwerte  f (0)  und  f (1) .
3. Welche Zahl übertrifft ihr Quadrat am meisten?
4. Der Umfang eines Kreisausschnittes sei  1 m  . Bei welchem Radius  r  wird der Flächeninhalt des Kreisausschnittes maximal?
5. Eine Kugel wird senkrecht nach oben geworfen und für die Höhe  h  gilt das
   Weg-Zeit-Gesetz  h (t) = 32 t - 5 t² .
   Wie hoch und wie lange steigt die Kugel?
6. Wie hoch ist der einer Kugel vom Radius  R  einbeschriebene Zylinder mit
   1. maximalem Volumen
   2. maximaler Mantelfläche?
7. Löse Aufgabe 6 für eine Halbkugel.
8. Welches Rechteck mit gegebenem Umfang  U  hat den größten Inhalt?
9. Einem gegebenen Dreieck ist ein möglichst großes Rechteck einzubeschreiben.
10. Einer Kugel mit dem Radius  R  ist ein quadratisches Prisma einzubeschreiben mit
    1. maximalem Volumen
    2. maximaler Mantelfläche?
11. Welches gleichschenklige Dreieck mit
    1. der Schenkellänge  1 
    2. dem Umfang  1 
    hat den größten Fächeninhalt?
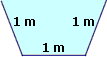
12. Wie breit muss ein Kanal oben sein, wenn er bei trapezförmigem Querschnitt nach nebenstehendem Bild möglichst großes Fassungsvermögen haben soll?
13. Ein regelmäßiges Pyramidenzelt mit maximalem Volumen soll aus
    1. drei
    2. vier
    3. sechs
    gleichlangen Stäben der Länge  3 m  erichtet werden. Wie hoch ist es?
14. Welche Maße hat die Pyramide maximalen Volumens mit der Oberfläche  1 m² ?
15. Das Netz einer quadratischen Pyramide ist aus einem Kreis vom Radius  R  auszuschneiden.
16. Einem Kegel mit dem Radius  R  und der Höhe  H  ist ein Zylinder
    1. maximalen Volumens
    2. maximaler Oberfläche
    einzubeschreiben.
17. Der von der Parabel  y = 9 - x²  und der x-Achse eingeschlossenen Fläche ist ein Rechteck maximalen Inhalts einzubeschreiben. Eine Rechteckseite liegt auf der x-Achse.
18. Welche Gerade durch  ( 2 | 8 )  bildet mit den Koordinaten-Achsen ein Dreieck kleinsten Flächeninhalts?
19. Welcher Punkt der Parabel  y = ¼ x²  hat vom Punkt  ( 0 | 2 )  den kleinsten Abstand?
20. Welcher Punkt der Parabel  y = 1/3 x²  hat vom Punkt  ( 9 | 0 )  den kleinsten Abstand?
21. Ein rechteckiges Grundstück an einem geraden Flussufer soll so von einem  100 m  langen Zaun eingezäunt werden, dass seine Fläche maximal wird.
22. Ein Draht der Länge  L  wird in zwei Teile zerschnitten, der eine wird zu einem Quadrat gebogen, der andere zu einem gleichseitigen Dreieck. Wie ist der Draht zu teilen, damit
    1. die Summe der Flächen maximal
    2. die Summe der Flächen minimal wird?
23. Die Tragfähigkeit eines Balkens von rechteckigem Querschnitt ist proportional zur Breite und zum Quadrat der Höhe. Welche Maße hat ein Balken höchster Tragfähigkeit, der sich aus einem zylindrischen Baumstamm vom Radius  r  schneiden lässt?
24. Für die geradlinige Bewegung eines Teilchens gilt das Weg-Zeit-Gesetz
    s = µ · t - ( 1 + µ⁴ ) · t² .
    Zeige: Das Teilchen bewegt sich zunächst vorwärts und kehrt schließlich um, wenn  µ > 0  ist. Für verschiedene  µ  kann sich das Teilchen höchstens um  1/8  vorwärts bewegen ( von t = 0 aus ).

weitere Aufgaben zu    9. Einführung in die Intergralrechnung  

 zurück zu MATHEMATIK Übersicht