Oberstufe: Differential- und Integralrechnung

Oberstufenskript Differential- und Integralrechnung für Grund- und Leistungskurse von Jürgen Rohde

zurück zum INHALT

 9.1 Inhaltsfunktion

 
9.2 Hauptsatz der Differential- und Integralrechnung

Wenn man die Beispiele in 9.1 auf der Suche nach Zusammenhängen zwischen einer Funktion und ihrer Inhaltsfunktion durchmustert, wird man eine erstaunliche Entdeckung machen:
 

H	Die Ableitung der Inhaltsfunktion ist gleich der Randfunktion,
	kurz:	I ' = (		) ' = f  .

Dies trifft in den Beispielen überall zu, außer an den Sprungstellen von  f , wo  I  nicht differenzierbar ist. Die Ausnahme stört. Andererseits sucht man eine möglichst "große" Klasse von Funktionen, für die die Aussage  H  richtig ist. Solche Funktionen dürfen offensichtlich keine Sprünge haben.
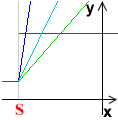Dieses Verbot würde in der Tat ausreichen, nur ist es mathematisch schwierig zu verarbeiten. Nebenstehende Abbildung zeigt, dass in einer Umgebung der Sprungstelle beliebig hohe Sekantensteigungen (evtl. dem Betrag nach) auftreten. Wenn man Funktionen betrachtet, bei denen die Sekantensteigungen dem Betrag nach beschränkt sind, verhindert man auch automatisch, dass Sprungstellen auftreten. Man erzwingt durch eine solche Forderung sozusagen einen "stetigen" Kurvenverlauf.

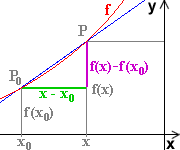
	Es sei  P0 ( x0 | f (x0) )  und  P ( x | f (x) ) . Die Steigung der Sekante ist
	f (x) - f (x0)
	x - x0
	Steigung ist beschränkt heißt: Für eine positive Zahl  L  ist
	|	f (x) - f (x0) x - x0	|  L    für alle x  U (x0) ;  x  x0

Die Überlegungen münden in folgende Definitionen:

	Definition   lokale L-Stetigkeit
	Die Funktion  f  heißt bei  x0   L-stetig , wenn es eine positive Zahl  L  gibt, so dass für alle  x  aus einer  U (x0)       | f (x) - f (x0) |   L · | x - x0 |    ist.
( L )	Definition   globale L-Stetigkeit
	Die Funktion  f  heißt im Intervall  [ a | b ]   L-stetig , wenn es eine positive Zahl  L  gibt, so dass      | f (x) - f (x0) |   L · | x - x0 |  für alle  x ,  x0      [ a | b ]  gilt.

Bemerkungen:

Die letztere Definiton ist zwar etwas weitergehender, sie wird jedoch vorgezogen, weil sie leichter zu handhaben ist, und weil die meisten hier interessierenden Funktionen die Eigenschaft  L  haben. Zu beachten ist die Äquivalenz für  x x0     |  f (x) - f (x0)  |   L          | f (x) - f (x0) |   L · | x - x0 |  x - x0 Die rechte Seite ist für  x = x0  ohnehin richtig. Deswegen zieht man diese Form in den Definitionen vor. Mit L-stetig sind folgende Begriffe synonym:   L-stetig   =   steigungsbeschränkt   =   dehnungsbeschränkt   Der Buchstabe  L  erinnert an den Mathematiker R. Lipschitz (1832 - 1903).

Beispiele

1. Alle Funktionen  f  mit  f (x) = m x + b  sind über    L-stetig.
   Denn  | m x + b - ( m x₀ + b ) | = | m | · | x - x₀ | .
2. Die Betragsfunktion  f (x) = | x | ist L-stetig in   .
   Denn  | | x | - | x₀ | | | x - x₀ |  ( L = 1 !)     (vergleiche 1.2   Satz 11).
3. Die quadratische Funktion  f (x) = x²  ist über jedem Intervall  [ a | b ]  wegen
    | x² - x₀² | = | x + x₀ | · | x - x₀ |    2 · max ( | a | ; | b | ) · | x - x₀ |  L-stetig.
   ( max ( | a | ; | b | )  bedeutet die größere der beiden Zahlen  | a | ; | b | .)

weiter zu    Einschließungssatz  

 zurück zu MATHEMATIK Übersicht