 |
Oberstufe: Differential- und Integralrechnung
|
Oberstufenskript
Differential- und Integralrechnung
für Grund- und Leistungskurse von Jürgen Rohde |
|
 zurück zum INHALT
zurück zum INHALT |
 9.2 Hauptsatz der Differential- und Integralrechnung
9.2 Hauptsatz der Differential- und Integralrechnung
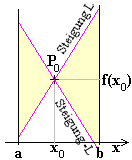
Da L-Stetigkeit über [ a | b ] bedeutet, dass alle Sekantensteigungen über
[ a | b ] zwischen -L und +L liegen, lässt sie sich sich durch
einen sehr instruktiven Einschließungssatz veranschaulichen.
 |
|
 |
| Bild 1 |
|
Bild 2 |
| f ist L-stetig in [ a | b ] |
Bild 1
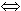 |
Durch jeden Punkt P0 ( x0 | f (x0) )
( x0 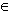 [ a | b ] ) [ a | b ] )
gibt es einen linearen Sektor,
welcher die Kurve von f über [ a | b ] verdeckt. |
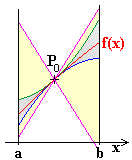
Man siehe zum Vergleich zurück nach 7.1 Satz 1
und vergleiche die Bilder 1 und 2 .
Bild 2 illustriert den Satz 1
| |
Satz 1 |
Wenn f in [ a | b ] L-differenzierbar, so auch L-stetig |
Denn wenn eine Funktionskurve durch einen quadratischen Sektor verdeckbar ist, so auch durch einen linearen,
Später wird ein algebraischer Beweis nachgeholt (siehe 10. Satz 2 ).
Die L-Stetigkeit erfüllt Linearitätseigenschaften
| |
Satz 2 |
f und g seien L-stetig in [ a | b ]
und c 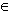 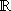 . .
Dann sind die Funktionen c · f und f + g ebenfalls L-stetig in [ a | b ] |
Beweis als Aufgabe 1 .
Die Aussage H (globale L-Stetigkeit)
soll nun für L-stetige Funktionen bewiesen werden.
 |
|
 |
| Figur 1 | Figur 2 |
Vorbemerkung:
| |
Die Funktion f sei L-stetig über [ a | b ] .
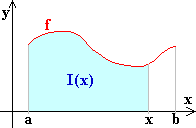
Es sei an dieser Stelle anschaulich plausibel vorausgestzt, dass es eine Funktion I gibt,
welche jedem x 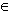 [ a | b ]
die Maßzahl der Fläche ( + oder - !) zwischen der Kurve von f und der x-Achse
über dem Intervall [ a | x ] zuordnet, in Zeichen [ a | b ]
die Maßzahl der Fläche ( + oder - !) zwischen der Kurve von f und der x-Achse
über dem Intervall [ a | x ] zuordnet, in Zeichen |
| |
x 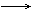 I (x) = I (x) = |
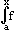 |
( Fig. 1) |
Es wird nun formuliert
| |
Satz 3 |
Hauptsatz der Differential- und Integralrechnung |
| Wenn f über [ a | b ] L-stetig ist, dann ist |
| I ' = ( |
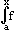 |
) ' = f . |
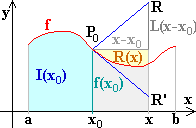
Beweis: Figur 2 verdeutlicht die Gleichung
| (1) |
I (x) = I (x0) + f (x0) · ( x - x0 ) + R (x) |
| |
| R (x) | ist beschränkt durch die Hälfte des Dreiecks P0 R R ' , also |
| (2) |
| R (x) |  ½ L ( x - x0 ) ²
½ L ( x - x0 ) ² |
| |
Aus (1) und (2) folgt die Behauptung I ' = f . |
Es empfiehlt sich sehr, die Definition der L-Differenzierbarkeit zu wiederholen
(im Abschnitt 5.2 Der Grundgedanke der linearen Approximation).
| Anmerkung: |
Statt |
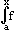 |
schreibt man sehr häufig |
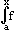 |
(t) dt . |
| |
Diese Bezeichnung geht zurück auf den Mathematiker und Philosophen Gottfried Wilhelm Leibniz (1646 - 1716).
Sie wird plausibel, wenn man daran denkt, dass Integrale von Treppenfunktionen durch Addition von Termen der Form
f (t) ·  t berechnet werden.
Im allgemeinen Fall ist an dieses Verfahren ein Grenzprozess anzuschließen,
symolisch ausgedrückt durch die Übergänge t berechnet werden.
Im allgemeinen Fall ist an dieses Verfahren ein Grenzprozess anzuschließen,
symolisch ausgedrückt durch die Übergänge |
| |
|
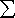 |
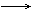 |
 |
und |
 t t
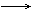 dt . dt . |
|
| Im Term |
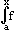 |
(t) dt spielen die Variablen |
x und t logisch gesehen ganz unterschiedliche Rollen: |
| |
Für x darf man jede Zahl aus [ a | b ] einsetzen,
x ist deshalb eine freie Variable.
t ist dagegen eine gebundene Variable.
Für t können keine reellen Zahlen eingesetzt werden.
Sinnlos sind Terme wie: |
| |
|
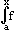 |
f (2) d2 |
weiter zu
Definition der Stammfunktion
 zurück zu MATHEMATIK Übersicht
zurück zu MATHEMATIK Übersicht




![]()