 |
Oberstufe: Differential- und Integralrechnung
|
Oberstufenskript
Differential- und Integralrechnung
für Grund- und Leistungskurse von Jürgen Rohde |
|
 zurück zum INHALT
zurück zum INHALT |
 9.2 Hauptsatz der Differential- und Integralrechnung
9.2 Hauptsatz der Differential- und Integralrechnung
Der Hauptsatz stellt die logische Verbindung her zwischen zwei Problemen,
die zunächst nichts miteinander zu tun zu haben scheinen:
dem Tangentenproblem und dem Flächenproblem.
Für L-stetige Funktionen gilt zumindest:
Das Flächenproblem ist im Wesentlichen gelöst,
wenn das Umkehrproblem zur Differentiation gelöst ist.
Diese Überlegungen motivieren folgenden Definition:
| | Definiton der Stammfunktion |
| F über D heißt Stammfunktion von f ,
wenn F ' = f in D . |
Z.B. sind alle Funktionen F (x) = ½ x² + C
( C aus 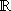 beliebig) Stammfunktionen von f (x) = x .
Weitere Stammfunktionen zu f gibt es auch nicht, wie der folgenden Satz zeigt:
beliebig) Stammfunktionen von f (x) = x .
Weitere Stammfunktionen zu f gibt es auch nicht, wie der folgenden Satz zeigt:
| | Satz 4 |
Satz über Stammfunktionen |
| Zwei Stammfunktionen F und G der Funktion f
unterscheiden sich nur um eine Konstante. |
Zum Beweis beachte man, dass G ' = F ' = f ist (Definition der Stammfunktion!). Daher ist
( G - F ) ' = G ' - F ' = f - f = 0 ,
also G - F eine Funktion, welche im Definitonsbereich die Ableitung Null hat.
Deswegen ist G - F nach Satz 4,
7.2 Globale Monotoniesätze, eine konstante Funktion.
Beispiele für Stammfunktionen
| Es sei f (x) = 2 x ; dann sind F (x) = |
 |
2 x dx = x² + C alle Stammfunktionen zu f . |
Künftig wird die Integralschreibweise häufig benutzt werden.
Man spricht in diesem Zusammenhang vom unbestimmten Integral.
- Wenn die Funktion f eine Stammfunktion hat, dann auch die Funktion a · f für
a
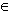
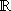 , und es gilt:
, und es gilt:
- Wenn f und g eine Stammfunktion haben, so auch f + g , und es gilt
 |
xn dx = |
1
n + 1 |
· xn+1 + C |
Für L-stetige Funktionen bzw. für alle Funktionen, zu denen es eine Stammfunktion gibt,
lassen sich die Werte der Inhaltsfunktion leicht berechnen. Dazu zunächst ein Beispiel.
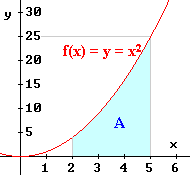
In der nebenstehenden Abbildung ist y = x² dargestellt.
Welche Maßzahl hat die blau getönte Fläche?
Nach Beispiel 4 (9.1 Inhaltsfunktionen) ist
I (x) = 1/3 x³ Inhaltsfunktion zu f über [ 0 | b ] .
Also ist
A = 1/3 5³ - 1/3 2³ = 117/3 = 39 .
| Werte von Inhaltsfunktionen heißen bestimmte Integrale. |
Allgemein gilt
| |
Satz 5 |
Hauptsatz der Integralrechnung |
Die Funktion f sei L-stetig in [ a | b ] .
F sei irgendeine Stammfunktion von f in [ a | b ] . |
| Dann ist |
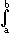 |
f = |
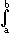 |
f (x) dx = F (b) - F (a) . |
|
Beweis:
| Nach dem Hauptsatz der Differenzial- und Integralrechnung ist |
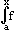 |
eine Stammfunktion von f . |
Nach dem Satz über Stammfunktionen gibt es eine Konstante C , so dass
| (1) |
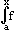 |
= F (x) + C für alle x
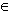 [ a | b ] . [ a | b ] . |
| Für x = a folgt |
a |
f = 0 = F (a) + C , also C = -F (a) |
 |
| a |
| Für x = b folgt |
b |
f = F (b) + C = F (b) - F (a) . |
 |
| a |
| Zur Vereinfachung wird folgender Term eingeführt: |
| F (b) - F (a) =def [ F (x) ] |
b |
|
| |
| a |
Zum Schluss wird der Intergrationsbegriff noch etwas verallgemeinert.
Bisher war die untere Integrationsgrenze kleiner als die obere. Diese Voraussetzung soll aufgegeben werden.
Zunächst sei a  c
c  b ,
f L-stetig in [ a | b ] und F Stammfunktion von f .
Dann ist (plausibel!)
b ,
f L-stetig in [ a | b ] und F Stammfunktion von f .
Dann ist (plausibel!)
| |
c |
f + |
b |
f = F (c) - F (a) + F (b) - F (c) = F (b) - F (a) = |
b |
f |
 |
 |
 |
| a |
c |
a |
und
| |
b |
f = F (b) - F (a) = - ( F (a) - F (b) ) = - |
a |
f . |
 |
 |
| a |
b |
Da von der gegenseitigen Lage von a, b und c kein Gebrauch gemacht wurde, gilt generell
| |
Satz 6 |
f sei L-stetig im Intervall I ,
F Stammfunktion von f
und a, b, c drei beliebige Zahlen aus I . Dann ist |
| |
b |
f = - |
a |
f und |
b |
f + |
c |
f = |
c |
f . |
 |
 |
 |
 |
 |
| a |
b |
a |
b |
a |
|
Aufgaben zu 9.2
weiter zu
9.3 Anwendungen der Integralrechnung
 zurück zu MATHEMATIK Übersicht
zurück zu MATHEMATIK Übersicht
![]() beliebig) Stammfunktionen von f (x) = x .
Weitere Stammfunktionen zu f gibt es auch nicht, wie der folgenden Satz zeigt:
beliebig) Stammfunktionen von f (x) = x .
Weitere Stammfunktionen zu f gibt es auch nicht, wie der folgenden Satz zeigt:

![]()