netSCHOOL AUFGABEN zu Differential-/Integralrechnung
[  I N H A L T  ]     [ MATHEMATIK Übersicht ]

Aufgaben zu
9.2 Hauptsatz der Differential- und Integralrechnung

  1. Beweise den Satz 2.
  2. Beweise: Wenn  f  L-stetig in  [ a | b ]  ist, dann ist auch  f  beschränkt in  [ a | b ] .
  3. Zeige:  f (x) = x³  ist L-stetig in  [ -1 | 3 ] .
  4. Zeige:  f (x) = xn  ist L-stetig in  [ a | b ] .
  5. Warum ist  f (x) = x²  über 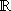nicht L-stetig?
  6. Warum sind ganzrationale Funktionen L-stetig über beliebigen endlichen Intervallen?
  7. Zeige: Die Funktion  x 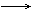1/x  ist über  [ 1 | 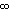[  L-stetig.
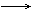
  8. Zeige: Die Funktion  x 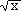ist L-stetig für alle  x 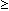a > 0 .
    ( Tip: 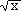  - 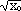 =   x - x0     (warum?)   )
    +
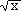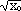  9. Bestätige:  f (x) · g (x)  -  f (x0) · g (x0)  =  f (x0) · [ g (x) - g (x0) ]  +  g (x) · [ f (x) - f (x0) ] .
    Beweise hieraus: Wenn  f  und  g  in  I  L-stetig sind, so auch  f · g .
  10. Gebe alle Stammfunktionen an
    Beispiel x² dx = 1/3 x³ + C       a.    ( 2 x + 3 ) dx
          b.    2 dx c. ( -3 ) dx
    d. 0 dx e. ( 1/2 x4 + 1/3 x2 + 2/5 x + 1 ) dx
    f. ( -x² + 2 x - 3 ) dx g. a xn dx
    h. xn+2 dx i. x2n dx
  11. Leite ab (nach  x )
          a.    x 2 t dt       b.    x 2 t dt       c.    x 2 v dv       d.    x 3 dv       e.    x dv       f.    x ( u + 2 )³ du
    2 -2 a a b c
  12. Leite die folgenden Integralfunktionen (= Inhaltsfunktionen) ab. Dabei sei vorausgesetzt, dass die Integranden stetig sind.
          a.    x      1    
    1 + 4 z²    		 dz             b.    x sin y dy             c.    x 2t dt
    1 - -1
  13. Beweise: Wenn  a, b  aus 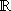und  f  und  g  über  I  L-stetige Funktionen sind gilt
                ( a · f  +  b · g )  =  a · f  +  b · g
  14. Löse in
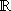
          a.    x t² dt = 29  2
    3    		             b.    4 ( 2 v - 3 ) dv = 5             c.    2x u3 du = 60
    2 x x
  15. Berechne die bestimmten Integrale
        a.    4 x² dx         b.    3 ( - 2 x³ + x - 1 ) dx         c.    -8 - 2 dx
    2 -1 -10
    d.    -1 dx e.    8 0 dx f.    -4 2 x dx
    4 5 -2
    g.    0 ( x - 1 )² dx h.    3 ( 4 x ³ + 6 x - 2 ) dx i.    8 ( x + 3 ) ( x - 3 ) dx
    1 -2 -4
    k.    4 ( 1/2 x² + 3 x + 5/6 ) dx l.    a ( x ³ - 7 x ) dx m.    -b ( x2 + 4 x4 + 8 ) dx
    2 -a b
  16. Welche Funktion hat an der Stelle  x  die Steigung  3 x²  und geht durch den Punkt  ( -1 | 1 ) ?
 

weitere Aufgaben zu    9.3 Anwendungen der Integralrechnung  

 zurück zu MATHEMATIK Übersicht