 |
AUFGABEN zu Differential-/Integralrechnung
|
Aufgaben zu
9.3 Anwendungen der Integralrechnung
- Bestimme die Fläche zwischen der Kurve zu y = f (x) über [ a | b ]
und der x-Achse.
| a. |
y = 3 x² + 1 , |
[ -1 | 3 ] |
|
b. |
y = -2 x² + x , |
[ 1 | 4 ] |
| c. |
y = ( 3 x + 4 )² , |
[ -3 | 0 ] |
d. |
y = - x³ , |
[ -3 | 3 ] |
| e. |
y = -2 x³ + 3 x² - 6 , |
[ 1 | 3 ] |
f. |
y = 2 x4 - x³ + 2 x² , |
[ -4 | -2 ] |
- Bestimme die Maßzahl der von der Kurve y = f (x) und der x-Achse eingeschlossenen Fläche.
| a. |
y = 16 - x² |
|
b. |
y = ( x + 4 ) ( x - 2 ) |
| c. |
y = ( x + 5 ) ( x + 3 ) ( x - 1 ) |
d. |
y = x³ - 2 x² |
| e. |
y = - ¼ x4 + 2x² + 12 |
f. |
y = - ¼ x4 + 2x² - 2 |
- Welche Fläche schließen die Funktionen f und g ein?
| a. |
f (x) = 2 - x² ; |
|
g (x) = - x |
| b. |
f (x) = 2 x - x² ; |
g (x) = - 3 |
| c. |
f (x) = x² ; |
g (x) = x |
| d. |
f (x) = x4 - 2 x² ; |
g (x) = 2 x² |
| e. |
f (x) = x³ - 9 x ; |
g (x) = 8 x |
| f. |
f (x) = 1/3 x³ + ½ x² - 6 x ; |
g (x) = Wendetangente |
- Beweise:
Wenn f und g über [ a | b ] stetig sind, dann ist
| |
b |
( f + g ) = |
b |
f + |
b |
g und |
b |
r f = r |
b |
f mit r
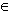
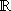 . . |
 |
 |
 |
 |
 |
| a |
a |
a |
a |
a |
- Beweise
Formel 1
in Abschnitt 9.3
für L-stetige Funktionen f und g ; beachte auch die Lage im Koordinatensystem!
-
 |
 |
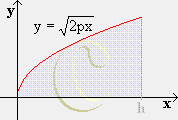 |
| Die in 6a bis 6e gemusterten Flächen sollen um die x-Achse rotieren.
Was für Körper entstehen?
Welchen Inhalt haben sie? |
 |
 |
- Die von der Kurve y = x - x² und der x-Achse eingeschlossene Fläche
soll um die x-Achse rotieren. Welches Volumen hat der entstehende Drehkörper?
- Das zwischen den Kurven y = 3 x - x² und y = x liegende Flächenstück
rotiere um die x-Achse. Volumen des Drehkörpers?
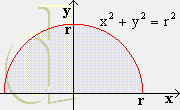
- Eine halbkugelförmige Schale mit Radius r ist bis zur Höhe h
mit Wasser gefüllt. Berechne das Wasservolumen.
- Nebenstehende Fläche werde um die y-Achse gedreht.
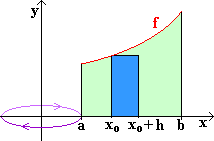
| Das Volumen des Drehkörpers sei |
V | b
a | . |
f sei L-stetig in [ a | b ] .
Das blaue Recheck erzeugt bei Drehung um die y-Achse einen Ring mit dem Volumen
VR = 2  ·
( x0 + h/2 ) · h · f (x0)
(warum?) .
·
( x0 + h/2 ) · h · f (x0)
(warum?) .
| Zeige weiter ( V | x
a |
) ' = 2  · x · f (x) · x · f (x) |
. |
( Formuliere den Rest und zeige, dass | R (h) |
 const. · h² ist. )
const. · h² ist. )
Dann ist
| 1 |
V |
b
a |
= 2  · · |
b |
x · f (x) dx . |
 |
| a |
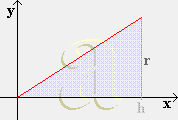
- Die von den Koordinaten-Achsen, der Kurve y = x³ und der Geraden y = h
eingeschlossene Fläche rotiere um die y-Achse.
Berechne das Volumen des Drehkörpers nach
1 aus Aufgabe 10.
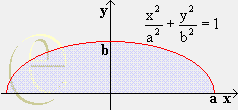
- Die von der Kurve y = - ¼ x4 + 2 x² + 12
und der Tangente durch ihre Hochpunkte eingeschlossene Fläche rotiere um die y-Achse.
Berechne das Volumen des Drehkörpers.
-
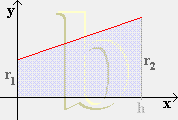
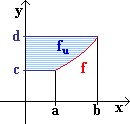 Die im Bild blau schraffierte Fläche rotiere um die y-Achse.
Die im Bild blau schraffierte Fläche rotiere um die y-Achse.
Dabei sei die Funktion f umkehrbar über [ a | b ] mit der Umkehrfunktion
fu über [ c | d ] .
f und fu seien stetig. Zeige dann
| 2 |
V |
d
c |
=  · · |
d |
fu (y)² dy . |
 |
| c |
- Die Flächen aus Aufgabe 6 sollen um die y-Achse rotieren.
Berechne die Volumina der Rotationskörper nach
2 Aufgabe 13.
-
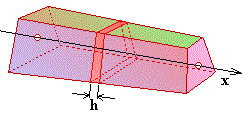 Die Inhalte vieler Körper lassen sich berechnen,
indem man sie zunächst gedanklich in Scheiben senkrecht zu einer geeigneten Achse zerlegt.
Wenn man die Größe jeder Querschnittfläche kennt,
lässt sich das Volumen des Körpers berechnen.
Die Inhalte vieler Körper lassen sich berechnen,
indem man sie zunächst gedanklich in Scheiben senkrecht zu einer geeigneten Achse zerlegt.
Wenn man die Größe jeder Querschnittfläche kennt,
lässt sich das Volumen des Körpers berechnen.
Zeige:
Wenn Q die L-stetige Querschnittsfunktion ist, dann ist
| 3 |
V |
b
a |
= |
b |
Q (x) dx . |
 |
| a |
- Berechne nach Aufgabe 15 das Volumen einer Kugel und eines Kugelabschnittes.
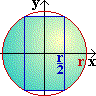
- Eine Kugel vom Radius r werde von einem Bohrer mit dem Durchmesser r durchbohrt.
Welchen Inhalt hat der Restkörper?
Berechne nach verschiedenen Methoden.
( Ergebnis: ½ 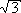
 · r³ )
· r³ )
- Berechne nach Aufgabe 15 das Volumen einer Pyramide mit der Grundfläche und der Höhe h .
- Die Querschnitte eines Körpers in zur x-Achse senkrechten Ebenen seien Kreise,
deren Durchmesser zwischen den Kurven
y = x² und y = 8 - x² liegen.
Der Körper liegt zwischen den Schnittpunkten dieser beiden Kurven.
( Ergebnis: 512/15
 )
)
- Die Grundfläche eines Körpers sei der Kreis x² + y² = r² .
Jede zur x-Achse senkrechte Ebene schneidet aus dem Körper ein Quadrat aus,
von dem eine Kante in der Grundfläche liegt.
Bestimme das Volumen des Körpers.
( Ergebnis: 16/3
 r³ )
r³ )
weitere Aufgaben zu
9.4 Die Existenz von Inhaltsfunktionen
 zurück zu MATHEMATIK Übersicht
zurück zu MATHEMATIK Übersicht


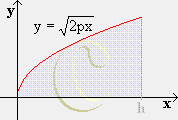



![]() ·
( x0 + h/2 ) · h · f (x0)
(warum?) .
·
( x0 + h/2 ) · h · f (x0)
(warum?) .
 Die im Bild blau schraffierte Fläche rotiere um die y-Achse.
Die im Bild blau schraffierte Fläche rotiere um die y-Achse.
 Die Inhalte vieler Körper lassen sich berechnen,
indem man sie zunächst gedanklich in Scheiben senkrecht zu einer geeigneten Achse zerlegt.
Wenn man die Größe jeder Querschnittfläche kennt,
lässt sich das Volumen des Körpers berechnen.
Die Inhalte vieler Körper lassen sich berechnen,
indem man sie zunächst gedanklich in Scheiben senkrecht zu einer geeigneten Achse zerlegt.
Wenn man die Größe jeder Querschnittfläche kennt,
lässt sich das Volumen des Körpers berechnen.

![]()