 |
AUFGABEN zu Differential-/Integralrechnung
|
Aufgaben zu
9.4 Die Existenz von Inhaltsfunktionen
- siehe im Text
- siehe im Text
- siehe im Text
- Führe den Existenzbeweis für das Volumen eines Rotationskörpers
unter der Voraussetzung einer stetigen Randkurve durch
analog zum Existenzbeweis des bestimmten Integrals.
- Verfahre ebenso wie in Aufgabe 4 bei der Fläche zwischen zwei Kurven.
- Führe ebenso den fehlenden Existenzbeweis zu Aufgabe 15 in 9.3 durch.
- Gegeben sei f (x) = x² in [ 2 | 4 ] .
Dieses Intervall werde in 1000 glichlange Teile zerlegt.
Um wieviel unterscheiden sich dann die Inhalte
der zugehörigen unteren und oberen Sägezahnkurve?
- Welchen Inhalt hat die verdeckende Dreieckskette der Kurve
y = 1/x über dem Intervall [ 1 | 3 ] ,
falls dieses in 10.000 Teile zerlegt wird?
(Zeige zunächst, dass L = 1 ist.)
- f sei eine stetige Funktion. Schreibe
| lim |
|
1
n |
[ f ( |
1
n |
) + f ( |
2
n |
) + . . . + f ( |
n
n |
) ] als bestimmtes Integral. |
n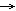 
 |
-
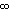| Berechne nach Aufgabe 9 |
lim |
|
1
n16 |
[ 115 + 115
+ . . . + n15 ] . |
| n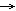
|
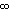weitere Aufgaben zu
10. Eigenschaften L-stetiger Funktionen
zurück zu MATHEMATIK Übersicht