 |
Oberstufe: Differential- und Integralrechnung
|
Oberstufenskript
Differential- und Integralrechnung
für Grund- und Leistungskurse von Jürgen Rohde |
|
 zurück zum INHALT
zurück zum INHALT |
 9.3 Anwendungen der Integralrechnung
9.3 Anwendungen der Integralrechnung
9.4 Die Existenz von Inhaltsfunktionen
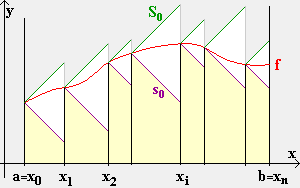
In diesem Abschnitt wird der zurückgestellte Existenzbeweis der Inhaltsfunktion L-stetiger Randkurven nachgeholt.
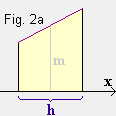
Die Funktion f sei über dem Intervall [ a | b ] L-stetig.
Das Intervall [ a | b ] wird durch die Zahlen
x0 = a , x1 , x2 ,
. . . , xi , . . . , xn = b
in endlich viele Teilintervalle zerlegt.
Die Menge 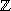 0 =
{ x0 , x1 , x2 ,
. . . , xn } heißt
Zerlegung von [ a | b ] .
0 =
{ x0 , x1 , x2 ,
. . . , xn } heißt
Zerlegung von [ a | b ] .
Wegen der L-Steigkeit von f über [ a | b ]
gibt es einen linearen Sektor, der die Kurve von f über [ a | b ] ,
erst recht über jedem Teilintervall verdeckt.
Davon benutzt man über den Teilintervallen nur den rechten Teil.
Dadurch erhält man zur Zerlegung 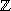 0
eine Kette von Dreiecken, welche die Kurve von f über
[ a | b ] verdeckt.
0
eine Kette von Dreiecken, welche die Kurve von f über
[ a | b ] verdeckt.
Anders ausgedrückt: Zur Zerlegung 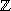 0
gibt es eine untere Sägezahnkurve s0 und eine
obere Sägezahnkurve S0 für f ,
0
gibt es eine untere Sägezahnkurve s0 und eine
obere Sägezahnkurve S0 für f ,
so dass s0
 f
f
 S0 in [ a | b ] ist.
S0 in [ a | b ] ist.
| Die Integrale |
b |
s0 und |
b |
S0 |
bestehen aus Inhalten von Trapezen, |
 |
 |
| a |
a |
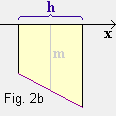
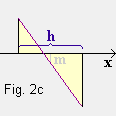
wobei auch überschlagene Trapeze wie in Fig. 2c vorkommen können.
Die Trapezinhalte können auch negativ sein wie in Fig. 2b und 2c.
Auf Grund der Konstruktion gilt
| 1 |
|
b |
s0
 |
b |
S0 |
und |
2 |
|
b |
S0 - |
b |
s0 |
 L · ( b - a ) · d ,
L · ( b - a ) · d , |
 |
 |
 |
 |
| a |
a |
a |
a |
wobei d = max ( xi - xi-1 ) , i = 1, 2, . . . , n ist.
Man beachte:
2 ist ein Maß für den Inhalt
der in Fig. 1 weiß gehaltenen verdeckenden Dreieckskette.
| Aufgabe 1 |
Bestätige Formel 2 . |
| Anmerkung: |
d ist Länge des längsten Teilintervalls.
Anschaulich ist klar, dass die zu definierende Flächenmaßzahl zwischen den Inhalten
der unteren und oberen Sägezahnkurve liegt und dass Formel 2
ein Maß für die "Genauigkeit" ist, die sich offenbar durch "feinere"
Zerlegung von [ a | b ] verbessern läßt. |
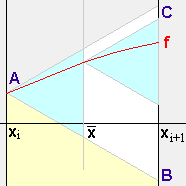 Um die Kurve von f enger durch Sägezahnkurven einzuschießen, konstruiert man aus der
Zerlegung
Um die Kurve von f enger durch Sägezahnkurven einzuschießen, konstruiert man aus der
Zerlegung  0 durch Hinzunehmen der
Mitten aller Teilintervalle die Zerlegung
0 durch Hinzunehmen der
Mitten aller Teilintervalle die Zerlegung  1 .
1 .
 1 heißt Verfeinerung von
1 heißt Verfeinerung von
 0 .
0 .
Die zugehörigen Sägezahnkurven seien mit s1 bzw. S1 bezeichnet.
Wie sich ihre Inhalte und deren Differenz gegenüber s0 bzw. S0
ändern, läßt sich an Hand von Fig. 3 beantworten.
Die Summe der Inhalte der hellblauen Dreiecke ist genau halb so groß wie der Inhalt
des Dreiecks ABC . Zeige dies im einzelnen.
Aufgabe 2 Zeige
| |
b |
s0  |
b |
s1  |
b |
S1  |
b |
S0 und |
b |
S1 - |
b |
s1 = ½ [ |
b |
S0 - |
b |
s0 ] = ½ L · d · ( b - a ) |
 |
 |
 |
 |
 |
 |
 |
 |
| a |
a |
a |
a |
a |
a |
a |
a |
Die Wiederholung dieser Gedankengänge führt zur Zerlegung
 i
mit den Sägezahnkurven si bzw. Si und es gilt:
i
mit den Sägezahnkurven si bzw. Si und es gilt:
| |
b |
s0  |
b |
s1  . . .
. . .  |
b |
si  . . .
. . .  . . .
. . .  |
b |
Si  . . .
. . .  |
b |
S2  |
b |
S2  |
b |
S0 |
 |
 |
 |
 |
 |
 |
 |
| a |
a |
a |
a |
a |
a |
a |
| und |
b |
Si - |
b |
si  |
1
2i |
· L · d · ( b - a ) . |
 |
 |
| a |
a |
| Also bilden die Intervalle [ |
 |
si | |
 |
Si ] eine Intervallschachtelung, |
bei der die Länge der Intervalle beliebig klein wird.
Nach dem Axiom der Intervallschachtelung gibt es eine (genau eine) Zahl,
die in allen Intervallen enthalten ist.
| Sie wird mit |
b |
f oder mit |
b |
f (x) dx bezeichnet |
 |
 |
| a |
a |
und man nennt sie das bestimmte Integral
der Funktion f von a bis b .
weiter zu
Bemerkungen
 zurück zu MATHEMATIK Übersicht
zurück zu MATHEMATIK Übersicht

![]() 0 =
{ x0 , x1 , x2 ,
. . . , xn } heißt
Zerlegung von [ a | b ] .
0 =
{ x0 , x1 , x2 ,
. . . , xn } heißt
Zerlegung von [ a | b ] .
![]() 0
gibt es eine untere Sägezahnkurve s0 und eine
obere Sägezahnkurve S0 für f ,
0
gibt es eine untere Sägezahnkurve s0 und eine
obere Sägezahnkurve S0 für f ,
![]() f
f
![]() S0 in [ a | b ] ist.
S0 in [ a | b ] ist.
 Um die Kurve von f enger durch Sägezahnkurven einzuschießen, konstruiert man aus der
Zerlegung
Um die Kurve von f enger durch Sägezahnkurven einzuschießen, konstruiert man aus der
Zerlegung ![]() i
mit den Sägezahnkurven si bzw. Si und es gilt:
i
mit den Sägezahnkurven si bzw. Si und es gilt:
![]()