Oberstufe: Differential- und Integralrechnung

Oberstufenskript Differential- und Integralrechnung für Grund- und Leistungskurse von Jürgen Rohde

zurück zum INHALT

 1.1 Ungleichungen

1.2 Betrag und Abstand

Zur Berechnung von Abständen definieren wir die folgende Funktion über  :

| a |  =

{

a ,   wenn  a 0 -a ,   wenn  a < 0

Lies: "Betrag von a"  oder  "a absolut"

Beispiel: | 3 | = 3 ;  | -3 | = 3

Geometrisch und einprägsamer:
    | a | ist gleich dem Abstand der Zahl  a  von  0 .

Folgende Eigenschaften der Betragsfunktion beweist man leicht durch Fallunterscheidungen und Beachtung der Definition:

Satz 9	1.   | a | 0   für alle a
	2.   - | a | a | a |   für alle a
	3.   | a | = | -a |
	4.   | a - b | = | b - a |   für alle a, b
	5.   | a · b | = | a | · | b |  und  | a : b | = | a | : | b |    für alle a, b
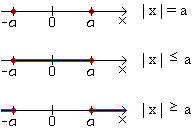
	6.   | x | = a x = a  oder  x = -a    für alle pos. a
	7.   | x | a -a x a -a x und x a x [ -a | a ]       Menge aller x , deren Abstand von 0 höchstens a ist.
	8.   | x | < a -a < x < a x ] -a | a [
	9.   | x | a x a oder x -a x \ ] -a | a [

Veranschaulichung der Lösungsmengen

Die Äquivalenzaussagen (6) bis (9) sind sehr nützlich beim Lösen von Gleichungen und Ungleichungen. Man beachte sehr genau und präge sich gut ein den Unterschied (und bzw. oder) bei (7) und (9). Vergleiche auch die Bilder.
Die Aussage " x a  oder  x -a " kann nicht zu einer Ungleichungskette vereinigt werden wie in (7).

Nun soll die bei Abschätzungen sehr häufig verwendbare Dreiecksungleichung bewiesen werden.
 

Satz 10

| a + b | | a | + | b |     für alle a, b

D.U.

Bemerkung: Der Name entstammt der Geometrie.
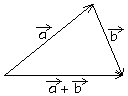
Im Dreieck ist die Summe zweier Dreiecksseiten größer als die dritte.

Beweis von D.U.:

1. Fall:	Es sei	a + b 0 .	Dann ist
	(1)	| a + b | = a + b	(vgl. Def. des Betrages)
	Weiter folgt	a | a | und b | b |
	durch Addition	a + b | a | + | b | ,
	was zusammen mit (1) nach dem transitiven Gesetz
		| a + b | | a | + | b |	ergibt.
2. Fall:	Es sei	a + b < 0 .	Dann ist
	(2)	| a + b | = -(a + b) = ( -a ) + ( -b )	(vgl. Def. des Betrages)
	Aus	( -a ) | a | und ( -b ) | b |
	folgt durch Addition der Ungleichungen
		( -a ) + ( -b ) | a | + | b | ,	was wegen (2)
		| a + b | | a | + | b |	besagt.
Aus der Dreiecksungleichung läßt sich z.B. eine Aussage über | a - b | herleiten:
	Aus	a = ( a - b ) + b
folgt nach der Betragsbildung aus der Dreiecksungleichung
		| a | = |( a - b ) + b | | a - b | + | b | ,
	also (3)	| a | - | b | | a - b |
und nach Vertauschung von a und b
		| b | - | a | | b - a | = | a - b |	oder
	(4)	-( | a | - | b | ) | a - b | .

Aus (3) und (4) folgt:

Satz 11

| | a | - | b | | | a - b |     für alle a, b

Merke:

| a - b | = | b - a |     ist der Abstand der Zahlen a und b .

Beispiele:
1.   Abstand von 3 und ( -5 ) ist | 3 - ( -5 )| = | 3 + 5 | = | 8 | = 8
2.   x² = 9 | x | = 3 x = 3 oder x = -3 = { 3; -3 }
3.   x² < 16 | x | < 4 -4 < x < 4
4.   x² 25 | x | 5 x 5 oder x -5 x \ ] -5 | 5 [
      Menge aller x , deren Abstand von 0 mindestens 5 ist.
5.   | x - 2 | 4; = Menge aller x , deren Abstand von 2 höchstens 4 ist = [ -2 | 6 ]
6.   | 2x + 6 | < 8 | x + 3 | < 4 | x - ( -3 ) | < 4
      = Menge aller x , deren Abstand von ( -3 ) kleiner als 4 ist.
7.   x² + 6 x + 5 > 0 ( x + 3 )² > 4 | x + 3 | > 2
      = Menge aller x , deren Abstand von ( -3 ) größer als 2 ist. = \ [ -5 | -1 ]
8.   x² + 6 x + 5 < 0 ( x + 3 )² < 4 | x + 3 | < 2 . = ] -5 | -1 [
9.   | 2x - 3 | = | x + 4 | ( 2x - 3 )² = ( x + 4 )² 3x² - 20x - 7 = 0

Aufgaben zu 1.2

weiter zu    1.3 Das Archimedische Axiom   

 zurück zu MATHEMATIK Übersicht