Oberstufe: Differential- und Integralrechnung

Oberstufenskript Differential- und Integralrechnung für Grund- und Leistungskurse von Jürgen Rohde

zurück zum INHALT

Thema des vorliegenden Skripts ist die Mathematisierung von Begriffen wie Bewegung und Veränderung. Mit solchen Gegenständen befasst sich die Analysis, die Lehre von den Funktionen. Sie besteht aus zwei Teilgebieten: der Differentialrechnung und der Integralrechnung. Letztere befasst sich mit Inhaltsproblemen oder der Addition beliebig vieler Summanden, erstere mit relativen Änderungen von Funktionswerten.

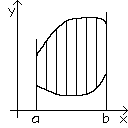
Inhaltsproblem	lineare Approximation - Tangente

Die einfachste Beziehung zwischen zwei Größen ist die Proportionalität, mathematisch zu beschreiben durch lineare Funktionen. Diese sind leicht zu überschauen und zu handhaben. Man wird also versuchen, beliebige Funktionen wenigstens stückweise durch lineare Funktionen anzunähern (approximieren). Dieses Programm heißt lineare Approximation. Dabei ergibt sich die Frage nach der Größe des Fehlers beim Ersatz einer Funktion durch eine geeignete lineare Funktion.

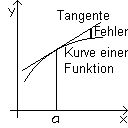
In der Sprache der Geometrie handelt es sich um das sog. Tangentenproblem.

Zur Vorbereitung des eigentlichen Programms werden Eigenschaften von Funktionen (linearen), Ungleichungen und Beträgen zusammengestellt.

1. Das Rechnen mit Ungleichungen und Beträgen

1.1 Ungleichungen

  sei die Menge der reellen Zahlen. Es genügt hier, sich darunter alle Zahlen vorzustellen, die sich in der Dezimaldarstellung schreiben lassen. Sie lassen sich auf einer Zahlengeraden darstellen und man kann in nach den bekannten Regeln über die Verknüpfungen  +  und  –  rechnen. Auf dieser Grundlage definieren wir in eine Relation  <  (Kleiner-Relation) durch die folgende Liste von Axiomen:

AO
AO1	Für je zwei reelle Zahlen  a, b  :
	Es gilt genau eine der Aussagen:  a < b ;   a = b ;   b < a .
	Trichotomie: In    lassen sich je zwei Zahlen vergleichen.
AO2	Für je drei reelle Zahlen  a, b, c  gilt:
	Wenn   a < b   und   b < c , dann  a < c  .
	Die Relation  <  ist transitiv.
AO3	Für je drei reelle Zahlen  a, b, c  gilt:
	Wenn   a < b , dann   a + c  <  b + c  .
	Die Relation  <  ist monoton bzgl.  +  .
AO4	Für je drei reelle Zahlen  a, b, c  gilt:
	Wenn  a < b  und  c > 0  , dann  a · c < b · c  .
	Die Relation  <  ist monoton bzgl.  ·  in + .

Bemerkungen:
Axiome sind Aussagen, die wir einerseits ohne Beweis akzeptieren, andererseits zur Herleitung weiterer Aussagen (Sätze), d.h. zum Aufbau einer Theorie verwenden.
⁺ ist die Menge der positiv reellen Zahlen.
Beachte in AO4, dass  c  positiv sein muss.
a < b   und   b < c   wird auch   a < b < c   geschrieben (Ungleichungskette).

Man veranschauliche sich die Axiome AO, indem man die dezimale Darstellung der reellen Zahlen oder deren Bilder auf dem Zahlenstrahl zu Grunde legt.
Die  < -Relation hat weitere interessante Eigenschaften, die sich aber alle auf die Axiome AO zurückführen lassen. Einige wichtige Eigenschaften werden wir als Beispiele beweisen, weitere finden sich in den Übungsaufgaben.

Übrigens beruht die Definition positiver Zahlen auf dem 1. Axiom:

a  heißt positive reelle Zahl, wenn  0 < a .
a  heißt negative reelle Zahl, wenn  a < 0 .

Weiter ist die Einführung einer zu  <  dualen Relation  >  (ist größer als) nützlich:

a > b   genau dann, wenn   b < a

Wir nennen und beweisen einige Sätze über die  < -Relation:

Satz 1	Für alle  a : wenn  a  negativ, dann  ( -a )  positiv.
	Denn aus  a < 0  folgt durch Addition von  ( -a )  nach dem 3. Axiom ( -a ) + a  <  0 + ( -a )   und daraus   0 < ( -a )
Satz 2	Wenn  a 0 , dann ist a² > 0  .
	Zum Beweis sei 1.  0 < a    durch Multiplikation der Ungleichung mit  a  folgt nach AO4:      0 < a² 2.  a < 0    dann ist ( -a ) > 0 , also nach 1. auch      ( -a )² = a² > 0 .
Man kann Ungleichungen addieren:
Satz 3	Wenn  a < b  und  c < d , dann  a + c < b + d .
	Beweis: Wenn  a < b , dann  a + c < b + c       nach AO3, wenn   c < d , dann  b + c < b + d       nach AO3. Weil  <  transitiv ist, folgt hieraus  a + c < b + d .
Über die Multiplikation einer Ungleichung mit negativen Zahlen gibt der folgende Satz Auskunft (vgl. Axiom AO4):
Satz 4	Wenn  a < b  und  c < 0 , dann  a · c >  b · c .
	Denn wegen  c < 0  ist nach Satz 1  ( -c ) > 0 . Aus  a < b  folgt dann nach dem 4. Axiom a · ( -c ) < b · ( -c) , d.h. -a · c < - b · c . Addiere a · c + b · c nach Axiom 3 . Es folgt  b · c < a · c , was mit  a · c > b · c  äquivalent ist.
Folgender Satz über die Multiplikation von Ungleichungen kann leicht selbst bewiesen werden.
Satz 5	Wenn  a < b ,  c < d  und  b > 0 ,  c > 0 , dann  a · c < b · d .
Die Axiome und weitere Eigenschaften der  < -Relation sind schon bekannt. Neu dürfte aber in diesem sehr überschaubaren Bereich die Erfahrung sein, was Beweisen in der Mathematik bedeutet. Es überrascht, dass man aus diesen Axiomen beweisen kann, dass 1 eine positive Zahl ist.
Satz 6	Es ist  1 > 0 .
	Denn wäre  1 < 0 , so wäre nach Satz 2   1² = 1 > 0 im Widerspruch zur Annahme 1 < 0 .
Satz 7	Wenn  a < 0 , dann auch  a -1 = 1/a < 0 .
	Denn aus  a < 0  folgt durch Multiplikation mit der nach Satz 2
	positiven Zahl    (  1 a  )² =   1 a²     die Behauptung.
Satz 8	Wenn  0 < a < b , dann  1/a > 1/b .
	Siehe Aufgabe 1 .

Die  < -Relation gestattet die Definition von Intervallen.
Abgeschlossenes Intervall	[ a | b ] = { x | a x b }
Offenes Intervall	] a | b [ = { x | a < x < b }
Entsprechend definiert man halboffene Intervalle	[ a | b [ oder ] a | b ] .

Aufgaben zu 1.1

weiter zu    1.2 Betrag und Abstand   

 zurück zu MATHEMATIK Übersicht