AUFGABEN zu Differential-/Integralrechnung

1. Das Rechnen mit Ungleichungen und Beträgen

Aufgaben zu
1.1 Ungleichungen

1. Beweise die Sätze 5 und 8 .
2. Von welchem Typ ist der Beweis von Satz 6 ?
    In welchem Zusammenhang ist Ihnen dieser Beweistyp bereits begegnet ?
 
3.  

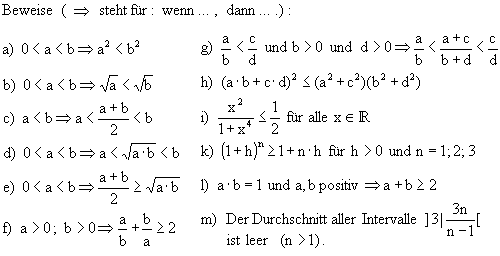
Aufgaben zu
1.2 Betrag und Abstand

5. Beweise alle Aussagen des Satzes 9 . 6. a) Zeichne x | x | über [ -5 | 5 ]     b) Zeichne x | 3x - 4 | über [ -4 | 4 ]     c) Zeichne x | x² - 9 | über [ -4 | 4 ] 7. Beweise für alle a, b     a) | a - b | | a | + | b |     b) || a | - | b || | a - b |     c) | a + b | + | a - b | | a | + | b |     d) | a + | a - | a ||| = | a |     e) | a - | a - | a ||| = 2 · | a | - a     f) max( a | b ) = ( a + b + | a - b | ) : 2 9. Begründe die einzelnen Schritte des folgenden Beweises der Dreiecksungleichung: - | a | a | a | ;  - | b | b | b | - ( | a | + | b | ) a + b | a | + | b |     | a + b | | a | + | b |

8. Löse in     a) | x - 3 | < 6     b) | x + 2 | 2,4     c) | 2x + 3 | 4     d) | -3x + 5 | < 8     e) | -2x - 5 | > 9     f) | 5x + 7 | > 1     g) x² - 3x - 4 > 0     h) x² - 3x - 4 < 0     i) 3x² + 12x + 15 0     k) 3x² + 12x + 15 0     l) 3 : ( x - 4 ) > 2     m) 5 : ( - 2x + 1) 1     n) x ( x + 1 ) ( x - 3 ) 0     o) ( x - a ) ( x - b ) < 0     p) x : ( x - 1 ) < 0     q) | 2x + 1 | = x - 2     r) | 3x - 8 | = | x - 1 |     s) | x² - 5 | 3

 

Aufgaben zu
1.3 Das Archimedische Axiom

10. Beweise den Satz 14
11. Beweise den Satz 15
12. Beweise: ( a und k ⁺ und | a | < k/n für alle n ) a = 0 .
13. Beweise: Falls a c/n ( c > 0 ) für alle n , so  a 0 .
14. Zeige die Äquivalenz der Sätze 13 und 14 mit Arch.
15. Darf man in Arch das  < -Zeichen durch das   -Zeichen ersetzen ?
 

weitere Aufgaben zu    2. Lineare Funktionen  

 zurück zu MATHEMATIK Übersicht