Oberstufe: Differential- und Integralrechnung

Oberstufenskript Differential- und Integralrechnung für Grund- und Leistungskurse von Jürgen Rohde

zurück zum INHALT

 15. Weitere Integrationsmethoden

 
15.2 Partielle Integration

		Die Produktenregel kann umgeformt werden zu
			u v ' = u v - u ' v
		wobei  u  und  v  Funktionen mit stetiger Ableitung über einem Intervall  [ a | b ]  seien. Dann existieren auch die Integrale auf beiden Seiten über  [ a | b ]  mit
			b  u · v '  =  [ u · v ]  b a   -   b  u ' · v a a	Regel der partiellen Integration

Beispiel:

Gesucht sei

b

ln x dx    .

a

v '

u

Schreibt man

b

ln x dx  =

b

dx  =   [ x · ln x ]

b a

-

b

x ·

1 x

dx  =   b ln b - a ln a - ( b - a )

1

·

ln x

a

a

a

Man kann die Regel natürlich auch unter Weglassung der Integrationsgrenzen zur Bestimmung von Stammfunktionen benutzen. Im Beispiel

ln x dx  =

1 · ln x dx  =   x · ln x -

x ·

1 x

dx   =  x · ln x - 1 + C

Beispiel:

x · sin x dx

Man setzt  u (x) = x  und  v ' = sin x ; dann ist  u ' (x) = 1  und  v (x) = - cos x . Es folgt:

x · sin x dx  =  - x cos x -

1 · ( - cos x ) dx  =  - x cos x + sin x + C

 
15.3 Integral von Umkehrfunktionen

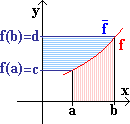
Die Funktion sei L-stetig und umkehrbar mit der Umkehrfunktion   . Anschaulich bestätigt man an Hand der Zeichnung leicht

		b	f  +	f (b)		=   b · f (b) - a · f (a)	Integralformel der Umkehrfunktion
		a		f (a)

Im folgenden Beweis sind die Argumente zu ergänzen:
Falls  f  zusätzlich L-differenzierbar ist, gilt

	b	f (x) dx  =	b	1 · f (x) dx  =  [ x · f (x) ]			b a	-	b	x · f ' (x) dx  =
	a		a						a
=				b · f (b) - a · f (a) -	b		( f (x) · f ' (x) ) dx
					a
=				b · f (b) - a · f (a) -	f (b)			(z) dz    ,
					f (a)

womit die obige Formel bewiesen ist.

Beispiel:

16		4		dy = 16 · 2 - 1 · 1 -	2	x4 dx =	4 5	· 31  ,
1					1

was man hier leicht durch direkte Integration kontrollieren kann. Die Integrationsformel funktioniert auch dann, wenn    nicht explizit angebbar ist.

Aufgaben zu 15.

weiter zu    16. Eigenschaften gebrochen rationaler Funktionen in Beispielen  

 zurück zu MATHEMATIK Übersicht