netSCHOOL AUFGABEN zu Differential-/Integralrechnung
[  I N H A L T  ]     [ MATHEMATIK Übersicht ]

Aufgaben zu
15. Weitere Integrationsmethoden

  1. Bilde Stammfunktionen

  2. Bilde Stammfunktionen

  3. Beispiel:

    Bearbeite analog

  4. Integriere durch geeignete Integration

  5. Bestimme Stammfunktion mittels partieller Integration
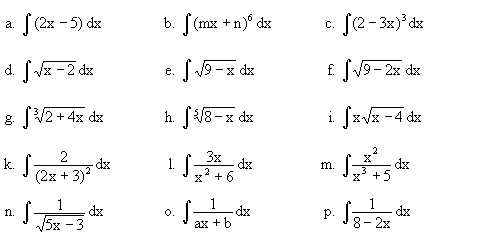
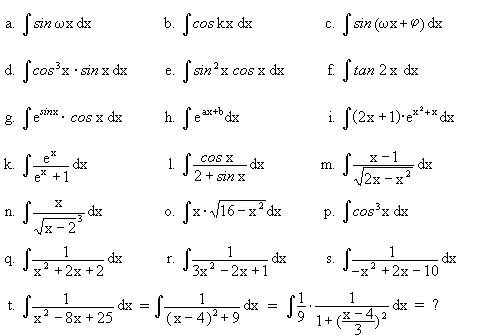
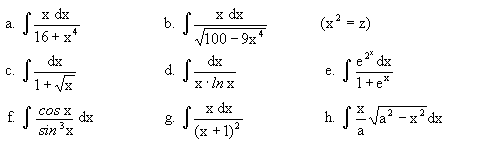
    a. ex · sin x  dx b. x · cos x  dx c. ex · cos x  dx
    d. x · ln x  dx e. x3 · ln x  dx f. (ln x )2  dx
    g. x2 · cos x  dx h. x4 · sin x  dx i. x · ex  dx
    k. sin2 x  dx l. sin3 x  dx m. sin4 x  dx
    n. x2 · e-x  dx o. arc sin x  dx p. arc tan x  dx

  6. Entwickle Rekursionsformeln für
    a. sinn x  dx b. cosn x  dx
    d. xn · ex  dx e. (ln x )n  dx

  7. Welchen Inhalt hat das von den beiden Kurven eingeschlossene Flächenstück für
    a.   y = x2 · e-x   und   y = e-x             b.   y = ln x   und   y = (ln x )2  .

  8. Beweise:   Die Inhalte der Flächenstücke zwischen der Kurve   y = e-x · sin x   und der x-Achse blden eine geometrische Folge.

  9.  
    Gegeben sei     f (x)  =   1 + 2 x          .
    ( x - 3 ) · ( x - 5 )

    Zeige, dass es Zahlen  a  und  b  gibt, so dass
            f (x) =     a  
    x - 3    		  +     b   
    x - 5    		     ist, und bestimme danach eine Stammfunktion von  f  .

    Verfahre ebenso für
    a.     f (x) =  2 x - 5       b.     f (x) =     1
    2 ( x + 4 ) · ( x - 2 ) x² - 1
    c.     f (x) =  x + 6   d.     f (x) =  6 x³ - 12 x² - 40 x - 2
    x² - 3 x² - 2 x - 8

  10. Bestimme  a, b, c  so dass
      f (x)  =   3 x² - 15 x + 8   =   a  +  b  +  c   gilt
    ( x - 1 )² ( x + 5 ) x - 1 ( x - 1 )² x + 5

    und daraus eine Stammfunktion von  f . Ebenso für
     a.    f (x) =  3 x² + 6 x - 1        b.    f (x) =  2 x² - 5 x + 1
    ( x + 1 ) ( x - 3 )² ( x + 1 )³

  11. Bestimme
          x² - x - 1  dx
    ( x - 2 ) ( x - 3 ) ( x - 4 )

 

weitere Aufgaben zu    16. Eigenschaften gebr. rationaler Funktionen  

 zurück zu MATHEMATIK Übersicht