 |
Oberstufe: Differential- und Integralrechnung
|
Oberstufenskript
Differential- und Integralrechnung
für Grund- und Leistungskurse von Jürgen Rohde |
|
 zurück zum INHALT
zurück zum INHALT |
 15. Weitere Integrationsmethoden
15. Weitere Integrationsmethoden
16. Eigenschaften gebrochen rationaler Funktionen
in Beispielen
Quotienten x  |
p (x)
q (x) |
ganzrationaler Funktionen heißen gebrochen rationale Funktionen. |
Sie sind offenbar überall dort definiert, wo der Nenner q (x) von Null verschieden ist.
Wichtig ist aber die Frage, wie sich diese Funktion in der Nachbarschaft derjenigen x-Werte verhält,
für die der Nenner 0 wird.
- Beispiel
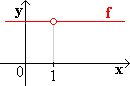
| f (x) = |
2 ( x - 1 )
x - 1 |
; x 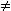 1 1 |
f ist an der Stelle 1 nicht definiert.
Für alle anderen x-Werte läßt sich der Bruch kürzen zu
f (x) = 2 ; x 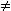 1 .
1 .
Der Graph von f ist also eine Parallele zur x-Achse, aber mit einer Lücke.
Man ist versucht die Lücke durch Hinzufügen des Punktes ( 1 | 2 ) auszufüllen.
Man sagt dafür auch, "die Funktion f sei stetig fortgesetzt."
- Beispiel
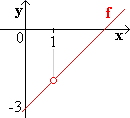
| Es sei f (x) = |
( x - 3 ) ( x - 1 )
x - 1 |
; |
|
| Auch hier hat f bei 1 eine Lücke und die stetige Fortsetzung |
| f * (x) = |
{ |
f (x) für x 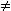 1 1 |
| - 2 für x = 1 |
- Beispiel
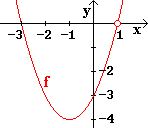
| Es sei f (x) = |
( x + 3 ) ( x - 1 )²
x - 1 |
Für x 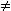 1 ist
f (x) = ( x + 3 ) ( x - 1 ) .
Die Lücke liegt auf der x-Achse,
hier spricht man von Lücke mit Vorzeichenwechsel.
1 ist
f (x) = ( x + 3 ) ( x - 1 ) .
Die Lücke liegt auf der x-Achse,
hier spricht man von Lücke mit Vorzeichenwechsel.
- Beispiel
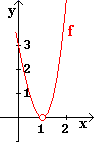
| Es sei f (x) = |
( x + 3 ) ( x - 1 )4
( x - 1 )² |
Für x 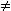 1 ist 1 ist |
| f (x) = |
( x + 3 ) ( x - 1 )² |
f hat bei 1 eine Lücke ohne Vorzeichenwechsel und
hat die stetige Fortsetzung f * , definiert durch
f * (x) = f (x) für
x 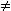 1 und
f * (1) = 0 (ohne Vorzeichenwechsel).
1 und
f * (1) = 0 (ohne Vorzeichenwechsel).
- Beispiel
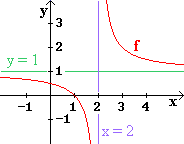
| Die Funktion f mit |
f (x) = 1 + |
( x - 2 )²
( x - 2 )³ |
( x 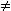 2 ) 2 ) |
| Nach dem Kürzen ist |
f (x) = 1 + |
1
( x - 2 ) |
bei 2 |
ebenfalls nicht definiert.
Je näher die x-Werte bei 2 liegen,
um so größer werden die Beträge der y-Werte,
und zwar erreichen sie von links beliebig negative Zahlen,
von rechts beiliebig hohe positive Zahlen.
Man sagt, " f hat bei 2
eine Polstelle oder Unendlichkeitsstelle mit Vorzeichenwechsel".
f kann bei 2 offenbar nicht stetig fortgesetzt werden.
Welchen Punkt man auch auf der Senkrechten zur x-Achse durch ( 2 | 0 )
hinzufügt, die Kurve bleibt unstetig.
Diese Senkrechte, also die Gerade x = 2 , hat in Bezug auf die Kurve von f
folgende Eigenschaft:
Wenn die x-Werte der Zahl 2 beliebig nahe kommen,
dann kommen die Punkte der Kurve von f der Geraden x = 2
beliebig nahe.
Sie heißt deshalb Asymptote der Kurve, genauer "senkrechte" Asymptote.
Übrigens auch die Gerade y = 1 ist Asymptote der Kurve,
denn für beliebig große | x | streben die y-Werte der Zahl 1 zu.
- Beispiel
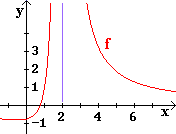
| Es sei f (x) = |
4 x - 3
( x - 2 )² |
f hat bei 2 eine Polstellen ohne Vorzeichenwechsel.
Ferner ist in diesem Beispiel die x-Achse Asymptote.
Dies gilt übrigens für alle echt gebrochenen rationalen Funktionen.
Das sind alle diejenigen gebrochenen rationalen Funktionen,
bei denen der Grad des Zählers kleiner als der Grad des Nenners ist .
Jede gebrochen rationale Funktion läßt sich - ggfs. durch Summendivision -
in eine ganzrationale und eine echt gebrochen rationale Funktion zerlegen.
Der ganzrationale Anteil heißt asymptotishe Kurve.
Die Diskussion gebrochen rationaler Funktionen umfasst auch die Bestimmung von Lücken,
Polstellen und Asymptoten.
Aufgaben zu 16.
- · -
 zurück zum INHALT
zurück zum INHALT
 zurück zu MATHEMATIK Übersicht
zurück zu MATHEMATIK Übersicht





