Oberstufe: Differential- und Integralrechnung

Oberstufenskript Differential- und Integralrechnung für Grund- und Leistungskurse von Jürgen Rohde

zurück zum INHALT

 13. Winkelfunktionen

 
14. Exponential- und Logarithmusfunktionen

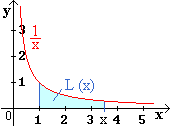
14.1 Integralfunktion zu   x 1/x

Die Integrationsregel

t n dt =

1    n + 1

t n+1 + C

versagt bei  n = - 1  . Daher ist jetzt noch keine Stammfunktion bekannt zu

x

1   x

,

obgleich leicht nachgewiesen werden kann, dass diese Funktion eine Stammfunktion hat, denn sie ist über jedem Intervall L-stetig, welches  0  nicht enthält. Also existiert die Funktion  L  mit

( 1 )	L (x) =	x	1    t	dt	für alle  x > t  .
		1

Eigenschaften der Funktion  L 
Trivialerweise gilt

( 2 )	L (0)  =	0   .
Wegen
( 3 )	L ' (x) =	1   x	> 0	( da  x > 0  !)

ist die Funktion  L  streng monoton steigend über ⁺  .
Die Funktion

	x L (k·x)  =	k·x	1    t	dt         für  k > 0 , x > 0
		1

ist nach der Kettenregel differenzierbar, und es gilt

[ L (k·x) ] ' = k · L ' (k·x) = k ·

1    k · x

=

1   x

,

d.h.  L (x)  und  L (k·x)  haben dieselbe Ableitung. Sie unterscheiden sich nur um eine Konstante  C   ,
also   L (k·x)  =  L (x) + C  .
Für  x = 1  folgt   L (1·k)  =  L (k) = L (1) + C = 0 + C = C ,
oder  L (k·x)  =  L (x) + L (k)
oder für beliebige  a , b > 0

( 4 )

L (a · b)  =  L (a) + L (b)

1. Funktionalgleichung von L

Aus

L ' (x r) = r · x r-1 ·

1  x r

=  r ·

1 x

folgt für alle  r   wie oben

1 r

· L (x r) = L (x) + C

,

wobei man für  C  hier Null erhält, wenn man für  x   1  wählt. Daher ist

( 5 )

L (x r)  =  r · L (x)

2. Funktionalgleichung von L

Wegen  L (2ⁿ) = n · L (2)  und  L (2^-n) = - n · L (2)  für alle  n   ist der Wertebereich von  L   .

Die Art der Funktionsgleichungen läßt vermuten, dass  L  eine logarithmische Funktion ist. Allerdings ist die Basis noch nicht bekannt. Sie ist bekanntlich definiert durch

L (Basis) = 1

Eine grobe Abschätzung erhält man, wenn man obige Abbildung auf Millimeterpapier zeichnet und eine Fläche vom Inhalt  1  abzählt. Der zugehörige  x-Wert ist ein Näherungswert für die Basis. Genauer und elegant erhält man die Basis, wenn man bedenkt, dass die Funktion  L  umkehrbar ist.

weiter zu    14.2 Die Umkehrfunktion von  L  

 zurück zu MATHEMATIK Übersicht