| Oberstufe: Differential- und Integralrechnung |
| Oberstufenskript Differential- und Integralrechnung für Grund- und Leistungskurse von Jürgen Rohde |
| Definition:
x0 heißt Nullstelle des Polynoms f (x), wenn f (x0) = 0 . |
| Für jedes Polynom f (x), welches nicht das Nullpolynom ist,
und für alle x0 |
|
| (1) | f (x) = f (x0) + ( x - x0 ) · g (x) |
| ist. Der Grad von g ist um 1 kleiner als der Grad von f . |
| Satz 1 | Wenn x0 Nullstelle des Polynoms f (x) ist,
dann ist f (x) durch ( x - x0 ) teilbar (ohne Rest). |
|---|---|
| Denn wegen (1) ist f (x) = ( x - x0 ) · g (x) . | |
| x - x0 heißt Linearfaktor zu x0 . | |
Aus Satz 1 folgt unmittelbar ( vgl. Aufgabe 15 )
| Satz 2 | Ein Polynom n-ten Grades hat höchstens n Nullstellen. |
|---|
Beispiel: Die Nullstellen von f (x) = 2 x4 + 4 x³ - 14 x² - 16 x + 24
Man sieht leicht, dass 1 Nullstelle ist:
| 2 | 4 | -14 | -16 | 24 | |||
|---|---|---|---|---|---|---|---|
| 2 | 6 | -8 | -24 | ||||
| x = 1 | | 2 | 6 | -8 | -24 | 0 | f (x) | = ( x - 1 ) · ( 2 x³ + 6 x² - 8 x - 24 ) |
| -4 | -4 | 24 | |||||
| x = -2 | | 2 | 2 | -12 | 0 | = ( x - 1 ) · ( x + 2 ) · ( 2 x² + 2 x - 12 ) | ||
| 4 | 12 | ||||||
| x = 2 | | 2 | 6 | 0 | = ( x - 1 ) · ( x + 2 ) · ( x - 2 ) · ( 2 x + 6 ) | |||
| -6 | |||||||
| x = -3 | | 2 | 0 | = 2 · ( x - 1 ) · ( x + 2 ) · ( x - 2 ) · ( x + 3 ) | ||||
Auf die angegebene Weise lassen sich höchstens ganzzahlige Nullstellen finden.
In der Regel ist man auf Näherungslösungen angewiesen,
vgl. z.B. die Kurve des Beispiels in 4.3 .
Wirksame Näherungsmethoden liefert die Differenzialrechnung.
Das Polynom f (x) = xn - x0n hat die Nullstelle x0. Das Horner-Schema ergibt:
| 1 | 0 | 0 | 0 | . . . | 0 | 0 | - x0n | |
| x0 | x0² | x0³ | . . . | x0n-2 | x0n-1 | x0n | ||
| x = x0 | | 1 | x0 | x0² | x0³ | . . . | x0n-2 | x0n-1 | 0 |
( Vergleiche auch Aufgabe 17 zu 3. vollständige Induktion )
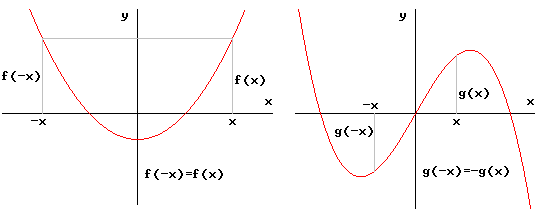
| Definition:
Die Funktion f heißt achsensymmetrisch bzgl. der y-Achse, wenn f (-x) = f (x) über D ( f heißt auch gerade ). Die Funktion g heißt punktsymmetrisch zum Ursprung oder ungerade, wenn g (-x) = -g (x) über D gilt. |
Symmetrische Funktionen haben besonders einfache Gestalt:
| Satz 3 | Wenn das Polynom
f (x) = a0 + a1 x + a2 x² + . . . + a2k x2k + a2k+1 x2k+1 + . . . + an xn ( 2 achsensymmetrisch ist, dann sind alle ai = 0 für ungerade i . |
|---|
a0 + a1 (-x) + a2 (-x)² + . . .
+ a2k (-x)2k + a2k+1 (-x)2k+1 + . . .
+ an (-x)n
=
a0 + a1 x + a2 x² + . . .
+ a2k x2k + a2k+1 x2k+1 + . . .
+ an xn
Aus dieser Gleichung fallen alle Terme mit geradem Index heraus. Man erhält schließlich
(2) 2 a1 x + 2 a3 x³ + . . . + 2 a2k+1 x2k+1 = 0
( 2 k + 1 = n oder 2 k + 1 = n - 1 )
für alle x ![]() .
.
Also ist jede reelle Zahl Nullstelle des Polynoms f (x) . Also ist nach Folgerung aus dem Satz
f (x) das Nullpolynom,
also sind
weiter zu
4.6 Beschränktheit von ganzrationalen Funktionen über Intervallen
![]()