Oberstufe: Differential- und Integralrechnung

Oberstufenskript Differential- und Integralrechnung für Grund- und Leistungskurse von Jürgen Rohde

zurück zum INHALT

 1.3 Das Archimedische Axiom

2. Lineare Funktionen

2.1 Wiederholung des Steigungsbegriffs

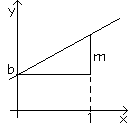Die Funktionen  x mx + b ( x ;   m, b ) heißen lineare Funktionen.

Ihr Bild in einem kartesischen Koordinatensystem ist bekanntlich eine Gerade mit der Steigung  m  und dem  y-Abschnitt  b ( Bild 1 ). Die Funktion  x mx + b  kann auch durch die (lineare) Funktionsgleichung  y = mx + b  beschrieben werden.

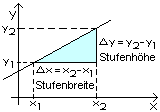
Die Bedeutung vom  m  wird so klar:   Wählt man
zwei beliebige Punkte P₁ ( x₁ | y₁ ) und P₂ ( x₂ | y₂ ) auf der Geraden y = mx + b  so gilt
y₁ = m · x₁ + b  und  y₂ = m · x₂ + b .
Für die Koordinatendifferenzen
x = x₂ - x₁ und y = y₂ - y₁ folgt
y = y₂ - y₁ = mx₂ + b - ( mx₁ + b ) = mx₂ - mx₁
     = m ( x₂ - x₁ ) = m ·x
Also ist  m = konstant, d.h. unabhängig von der Wahl der Punkte P₁ und P₂ .
Zur Wiederholung:

Steigung der Geraden = m =

Beachte: x ist kein Produkt. ist ein Operator oder Befehl.

Für alle Geraden gilt also:

y = m · x

y ist proportional x

Beispiel: Welche Steigung hat die Gerade durch

a.   P1( 3 | 2 ) und P2( -2 | -4 ) ?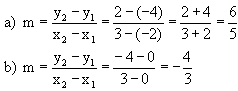
b.   durch den Ursprung ( 0 | 0 ) und den Punkt ( 3 | -4 ) ?

2.2 Sonderfälle

a) b = 0  y = mx  sind Ursprungsgeraden. Hier ist (sogar) y proportional zu x .
b) m = 0 y = b
    Die Abbildung x b ( ) heißt konstante Funktion.
    Ihr Bild ist eine Parallele zur x-Achse.
c) m = 0 und b = 0 y = 0   heißt Nullfunktion.
    Ihr Bild ist die x-Achse. Sie hat überall den Wert 0 .
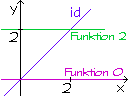
d) Die Funktion x x ( ) ( y = x ) heißt identische Funktion id .
e) Parallele Geraden haben die gleiche Steigung.

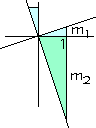
f) Bestätige am Bild:

Zwei Geraden y = m₁x + b₁ und y = m₂x + b₂ schneiden sich genau dann rechtwinklig, wenn m₂ = - ¹/m₁ ist.

2.3 Die Gleichung ax + by + c = 0

a)	b 0 y = -a/b x - c/b
	Bild der Lösungsmenge ist die Gerade mit der Steigung - a/b und dem y-Abschnitt - c/b .
b)	b = 0 und a 0 x = - c/a
	Bild der Lösungsmenge ist eine Parallele zur y-Achse. Solche Geraden haben keine Steigung. Die Stufenbreite x ist immer Null und der Quotient ohne Sinn. Beachte dagegen: Parallelen zur x-Achse haben eine Steigung und zwar 0/x = 0 .
c)	a = 0 und b = 0 und c 0 = Ø
d)	a = 0 und b = 0 und c = 0 0 · x + 0 · y + 0 = 0  ist allgemeingültig in

 

2.4 Punkt-Steigungsform, Zwei-Punkteform der Geradengleichungen

Beispiel:
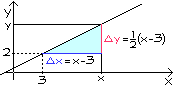Wie lautet die Gleichung der Geraden durch den Punkt P ( 3 | 2 ) mit der Steigung 1/2 ?
( x | y ) sei ein beliebiger (zweiter) Punkt der Gerade. Aus dem Bild entnimmt man  y = 2 + 1/2 (x - 3) = 1/2 x + 1/2 .
Wie lautet allgemein die Gleichung der Geraden durch den Punkt ( x₁ | y₁ ) mit der Steigung m ?
Zur Lösung sei ( x | y ) wieder ein beliebiger (zweiter Punkt) Punkt der Geraden. Dann ist

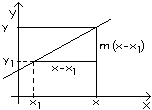	y = y1 + m ( x - x1)
	Punkt-Steigungs-Form der Geradengleichung

Wie lautet die Gleichung der Geraden durch die beiden Punkte  ( x₁ | y₁ ) und  ( x₂ | y₂ ) ?

Die Gerade hat die Steigung m =

. Also lautet die Gleichung der Geraden

	y = y1 +		( x - x1 )
	Zwei-Punkte-Form der Geradengleichung

Beispiele:
1.	Die Gerade  2 x + 3 y - 6 = 0  hat wegen  y = -2/3 x + 2  die Steigung  (-2/3)  und den y-Abschnitt  2  .
2.	Wie lautet die Gleichung der Geraden durch ( 6 | -2 ) und ( -4 | -8 ) ?
	Lösung:        y = -2 +	-8 - ( -2 )	( x - 6 ) = -2 + 3/5 ( x - 6 ) = 3/5 x - 28/5
		-4 - 6
3.	Wie lautet die Gleichung der Geraden. die durch ( 2 | 3 ) geht und auf der Geraden y = 2/3 x - 2 senkrecht steht?
	Lösung:   Die Steigung der gesuchten Geraden ist der Kehrwert der negativen Steigung 2/3; also m = -3/2. Daher ist   y = 3 - 3/2 ( x - 2 ) = - 3/2 x + 6   ihre Gleichung.

Aufgaben zu 2.

weiter zu    3. Das Beweisverfahren der vollständigen Induktion  

 zurück zu MATHEMATIK Übersicht