| |
 |
|
|
| MATHE Sinusfunktion |
| |
MATHE Schritt für Schritt
Alle Dreiecke lassen sich in rechtwinkelige Dreiecke aufteilen.
Im rechtwinkeligen Dreieck definiert man folgendes:
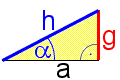Der Sinus eines Winkels ( α ) ist das Verhältnis
von Gegenkathete ( g ) zu Hypothenuse ( h ).
Wählt man die Hypothenuse zu 1 so ist die Gegenkathete direkt ein Maß für den Sinus.
Am besten läßt sich die Sinusfunktion am Einheitskreis veranschaulichen.
Alle Punkte des Einheitskreises haben den Abstand 1 vom Ursprung des Koordinatensystems.
Der Strahl (Hypothenuse) zu einem beliebigen Punkt des Kreises bildet mit der x-Achse den Winkel
α.
Der y-Wert (Gegenkathete) jedes Kreispunktes entspricht somit dem Sinus von α
| LAUF !
Der Bogen des Einheitskreises ist sensitiv ! |
 |
 |
| Bogenmaß b (rad) |
Winkel α (deg) |
sin(α) |
|
|
|
|
|
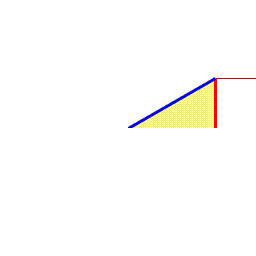
In der Abbildung oben finden wir den Einheitskreis im grünen ersten Koordinatensystem.
In Abhängigkeit vom Winkel α
verändert sich der y-Wert = Sinus (Höhe des gelben Bereichs).
Dieser wird nach rechts in das zweite Koordinatensystem
übertragen und dort als Funktion des Winkels dargestellt.
Das Bogenmaß mit der Einheit rad (Radiant) wird auch angezeigt (grün).
Der Link führt zur Definition des Bogenmaß.
Der Sinus ist eine der trigonometrischen Funktionen,
der Link führt zu den Definitionen und Eigenschaften.
MATHE Schritt für Schritt
zurück zu MATHEMATIK
Werner Plack
