
 |
|||
| MATHE Ausklammern | |||
AUSKLAMMERN oder FAKTORISIEREN
Schritt für Schritt
In vielen Situationen ergibt sich die Notwendigkeit Terme oder Gleichungen dadurch zu vereinfachen oder einen weiteren sinnvollen Lösungsweg einschlagen zu können, dass man ausklammert, das heißt nichts anderes als gemeinsame, in verschiedenen Ausdrücken gleichzeitig vorhandene Faktoren vor eine Klammer zu setzen und in der Klammer die Beträge zu schreiben, die durch Division der ursprünglichen Werte durch die ausgeklammerten Faktoren entstanden sind. Aus einer Summe oder Differenz ist dann ein Produkt mit zwei Faktoren geworden, daher der Begriff Faktorisieren. Das hört sich kompliziert an, ist aber ganz einfach, wenn man es durchführt. Einzige Voraussetzung ist, dass man dividieren (teilen) kann und die Rechenzeichen des ursprünglichen Terms nicht verändert, da ja sonst die Rechenaufgabe nicht mehr dieselbe bleibt wie vor dem Ausklammern.
Beispiel:
| Term: | 4 + 8 + 7 + 16 − 12 |
|---|
Die Rechnung ist natürlich sehr einfach ohne Ausklammern zu lösen, aber es geht hier um das Prinzip, das man an einfachen Zahlen leicht durchschauen kann:
Als größter gemeinsamer Faktor von 4 der 5 Zahlen ist die 4 sofort erkennbar, bei der 7 zwar nicht, aber sie ist prinzipiell auch durch 4 teilbar, also kann man die 4 ausklammern:
| 4 · ( 1 + 2 + 7/4 + 4 − 3 ) |
|---|
in der Klammer bleiben die Zahlen, die sich ergeben, wenn die ursprünglichen Zahlen durch 4 geteilt worden sind. Die Rechenzeichen dazwischen bleiben erhalten.
Der Wert des neuen Terms ist identisch (äquivalent oder gleichwertig) mit dem Wert des alten Terms, man hat also nur die Schreibweise geändert, es ist eine sogenannte Äquivalenzumformung geschehen.
Das lässt sich leicht überprüfen, indem man die Klammer wieder mit der 4 multipliziert. Das Ausmultiplizieren wird dabei vorausgesetzt. Das Ergebnis ist wieder der alte Term:
| 4 · 1 + 4 · 2 + 4 · 7/4 + 4 · 4 − 4 · 3 = 4 + 8 + 7 + 16 − 12 |
|---|
Man hätte natürlich auch den Faktor 2 ausklammern können,
wenn es im Zusammenhang mit dem Lösungsweg sinnvoll gewesen wäre.
Ob Ausklammern sinnvoll ist oder nicht und welcher Faktor ausgeklammert wird,
ist also vom Ziel der Rechnung abhängig, die ich zu einem Ergebnis bringen möchte.
Wenn man zum Beispiel die
| Gleichung | 15xy + 6yz = 3y |
|---|---|
| hat, kann man auf der linken Seite als gemeinsamen Faktor 3y ausklammern und erhält: | |
| 3y · (5x + 2z) = 3y | |
| so dass man durch 3y auf beiden Seiten teilen kann: | |
| 5x + 2z = 1 | |
Die Vereinfachung ist erkennbar, es ist y entfallen und die Zahlen sind kleiner.
In höheren Klassenstufen werden die Vorteile durch Ausklammern noch ersichtlicher, wenn beispielsweise Gleichungen 3. Grades gelöst werden sollen:
| x3 + 2x2 − 3x = 0 | |
|---|---|
| Ausklammern von x | x · ( x2 + 2x − 3 ) = 0 |
ergibt ein Produkt auf der linken Seite.
Weil ein Produkt 0 ist, wenn einer oder beide Faktoren 0 ist, ergibt sich als
| 1. Lösung: | 2.und 3. Lösung: | ||
|---|---|---|---|
| x1 = 0 | x2 + 2x − 3 = 0 | ||
| aus dem ersten Faktor | aus dem zweiten Faktor | ||
| der dann ausgerechnet werden muss nach der pq-Formel: |
|||
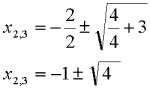 x2,3 = −1 ± 2 |
|||
| also gibt es die beiden weiteren Lösungen: | |||
| x2 = 1 und x3 = −3 | |||
| 2 Beispiele zum
AUSKLAMMERN |
| oben | home | Inhalt: |
web design: |
2008 | zurück |